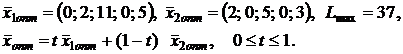Семинар 9. Симплексный метод решения

Симплексный метод является универсальным методом решения задач линейного программирования, так как позволяет решить практически любую задачу, представленную в каноническом виде.

Идея симплексного метода заключается в том, что, начиная с некоторого опорного решения, осуществляется последовательно направленное перемещение по опорным решениям системы к оптимальному опорному решению. Значение целевой функции при таком перемещении для задачи на максимум не убывает, на минимум не возрастает. Так как число опорных решений конечно, то через конечное число шагов оптимальное решение будет найдено.

Алгоритм симплексного метода

1. Привести задачу к каноническому виду.

2. Найти неотрицательное базисное решение системы ограничений.

3. Рассчитать оценки свободных переменных по формуле

,

где - коэффициенты при свободной переменной х_j,

- коэффициенты при базисных переменных в целевой функции,

- коэффициент при свободной переменной в целевой функции.

4. Проверить найденное опорное решение на оптимальность:

а) если все оценки D_j ³ 0 , то найденное решение оптимально и задача решена;

б) если хотя бы одна оценка D_j < 0, а при соответствующей переменной х_j нет ни одного положительного коэффициента, то задача не имеет оптимального решения из-за неограниченности целевой функции;

в) если хотя бы одна оценка D_j < 0, а при соответствующей переменной х_j есть хотя бы один положительный коэффициент, то найденное решение не оптимально и его можно улучшить, выполнив переход к новому базису. Если отрицательных оценок несколько, то в базис ввести переменную с наибольшей по абсолютной величине отрицательной оценкой.

Замечание 1. Критерием оптимальности для ЗЛП на минимум является неположительность оценок, т.е. все D_j £ 0, .

Замечание 2. В ЗЛП максимум и минимум целевой функции понимаются как глобальные.

Пример 1. Найти наибольшее значение функции

при ограничениях:

х₁-2х₂ - 2х₃ +х₄ - х₅ = 1,

-2х₂ - х₃ +3х₄ + 2х₅ = 5,

х₂ + 8х₃+ х₄ +3х₅ = 20,

.

Решение. Задача имеет канонический вид. Найдем исходное опорное решение.

Б.п.	х1	х2	х3	х4	х5	bi
x1	1 0 0	-2 -2 1	-2 -1 8	1 3 1	-1 2 3	1 5 20
x1 x2	1 0 0	0 0 1	14 15 8	3 5 1	5 8 3	41 45 20
x1 x5 x2	1 0 0	0 0 1	37/8 15/8 19/8	-1/8 5/8 -7/8	0 1 0	103/8 45/8 25/8

.

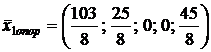Проверим это решение на оптимальность.

сj	Б.п.	1	1	-5	2	1	bi
		х1	х2	х3	х4	х5
1 1 1	x1 x5 x2	1 0 0	0 0 1	37/8 15/8 19/8	-1/8 5/8 -7/8	0 1 0	103/8 45/8 25/8
Dj		0	0	111/8	-19/8	0	173/8

Найденное решение не оптимально, так как D₄ < 0. Введем в базис свободную переменную с отрицательной оценкой х₄ .

сj	Б.п.	1	1	-5	2	1	bi
		х1	х2	х3	х4	х5
1 2 1	x1 x4 x2	1 0 0	0 0 1	5 3 5	0 1 0	1/5 8/5 7/5	14 9 11
Dj		0	0	21	0	19/5	43

. Так как среди оценок нет отрицательных чисел, то второе опорное решение оптимально.

, .

Пример 2. Найти наибольшее значение функции

при ограничениях:

х₁ + х₂ ³ 5,

2х₁ - х₂ £ 6,

2х₁ - 3х₂ ³-18,

.

Решение. Приведем задачу к каноническому виду, для этого в каждое неравенство введем балансовую переменную.

х₁ + х₂ - х₃ = 5,

2х₁ - х₂ + х₄ = 6,

2х₁ - 3х₂ - х₅ = -18,

.

Найдем исходное опорное решение:

Б.п.	х1	х2	х3	х4	х5	bi
х4 х5	1 2 -2	1 -1 3	-1 0 0	0 1 0	0 0 1	5 6 18
х2 x4 x5	1 3 -5	1 0 0	-1 -1 3	0 1 0	0 0 1	5 11 3

.

Проверим это решение на оптимальность, для этого найдем оценки свободных переменных в симплексной таблице:

сj	Б.п.	5	7	0	0	0
		х1	х2	х3	х4	х5	bi
7 0 0	х2 x4 x5	1 3 -5	1 0 0	-1 -1 3	0 1 0	0 0 1	5 11 3	- не оптимально, так как Δ3 = -7 < 0.
Dj		2	0	-7	0	0	35
7 0 0	х2 x4 x3	-2/3 4/3 -5/3	1 0 0	0 0 1	0 1 0	1/3 1/3 1/3	6 12 1	- не оптимально, так как Δ1 < 0.
Dj		-29/3	0	0	0	7/3	42
7 5 0	х2 x1 x3	0 1 0	1 0 0	0 0 1	½ 5/4 5/4	½ ¼ ¾	12 9 16	- оптимально, так как Δj ≥ 0,
Dj		0	0	0	29/4	19/4	129

, .

Отбросим балансовые переменные, получим оптимальное решение исходной задачи: , .

Задачи

1.

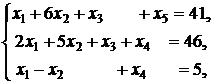
2.

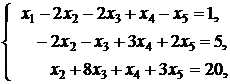
3.

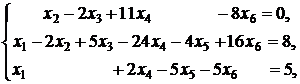
4.

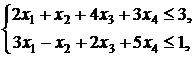
5.

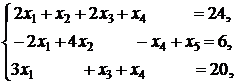
6.

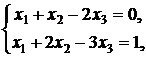
7.

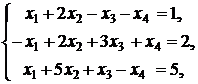
8.

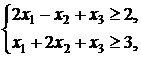
9.

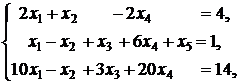
Ответы

1.

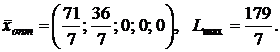
2.

3.

4.

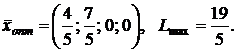
5.

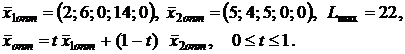
6. Задача не имеет оптимального решения из-за неограниченности целевой функции.

7. Задача не имеет оптимального решения из-за несовместности системы ограничений.

8.

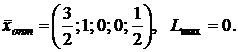
9.