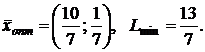Семинар
8. Графический метод решения
Графическим методом можно решать задачи
линейного программирования с двумя переменными, представленные в неканоническом виде, или сводящиеся к ним.
Рассмотрим следующую задачу: найти экстремум функции
![]()
при ограничениях:
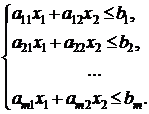
х1³0, х2³0.
Решение задачи начинают с
построения области допустимых решений. При этом возможны следующие случаи:
1. Область допустимых решений - пустое
множество. В этом случае задача линейного программирования не имеет оптимального решения из-за несовместности
системы ограничений.
2. Область допустимых решений
- единственная точка. Тогда задача линейного программирования имеет единственное и оптимальное решение.
3. Область допустимых решений
- выпуклый многоугольник. В этом случае, чтобы найти оптимальное решение
задачи, можно найти координаты всех угловых точек многоугольника, вычислить
значения целевой функции во всех угловых точках и выбрать наибольшее (или
наименьшее) из этих значений. Координаты соответствующей угловой точки являются
оптимальным решением.
Существует и другой способ,
который позволяет сразу найти графически угловую точку, соответствующую
оптимальному решению.
Пусть с0 - некоторое число. Прямая ![]() является линией
уровня целевой функции. В каждой точке этой прямой целевая функция принимает
одно и то же значение, равное с0. Вектор
- градиент целевой функции
является линией
уровня целевой функции. В каждой точке этой прямой целевая функция принимает
одно и то же значение, равное с0. Вектор
- градиент целевой функции
![]()
перпендикулярен
линиям уровня и показывает направление, в котором эта функция возрастает
с наибольшей скоростью. Выбирая из линий уровня, проходящих через область
допустимых решений, наиболее удаленную в направлении вектора ![]() (в случае
минимизации - в противоположном
направлении), определим угловую точку, в которой целевая функция принимает
максимальное (минимальное) значение. Если экстремум достигается сразу в
двух смежных угловых точках, то, по теореме об альтернативном оптимуме,
оптимальным решением будет любая точка отрезка, соединяющего эти точки:
(в случае
минимизации - в противоположном
направлении), определим угловую точку, в которой целевая функция принимает
максимальное (минимальное) значение. Если экстремум достигается сразу в
двух смежных угловых точках, то, по теореме об альтернативном оптимуме,
оптимальным решением будет любая точка отрезка, соединяющего эти точки:
![]() ,
, ![]() .
.
4. Область допустимых решений - выпуклая
неограниченная область.
В этом случае экстремум может
не существовать из-за неограниченности целевой функции сверху в задаче на
максимум, т.е.![]() , или снизу в задаче на минимум, т.е.
, или снизу в задаче на минимум, т.е. ![]() , или находиться в одной из угловых точек области допустимых
решений.
, или находиться в одной из угловых точек области допустимых
решений.
Алгоритм
графического метода
1. Построить область допустимых
решений.
2. Построить вектор-градиент целевой
функции ![]() .
.
3. Построить семейство линий уровня,
перпендикулярных вектору ![]() , проходящих через область допустимых решений.
, проходящих через область допустимых решений.
4. Выбрать линию уровня, проходящую
через область допустимых решений и наиболее удаленную в направлении вектора ![]() (или в
противоположном вектору
(или в
противоположном вектору ![]() направлении - в
задаче на минимум). Определить угловые точки области, через которые она проходит.
направлении - в
задаче на минимум). Определить угловые точки области, через которые она проходит.
5. Найти координаты точек экстремума
и значение целевой функции в этих точках.
Пример 1. Найти наименьшее и наибольшее
значения функции ![]() при
ограничениях:
при
ограничениях:
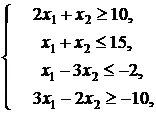
![]()
Решение.
1) Строим область допустимых
решений (ОДР). Она представляет собой выпуклый четырехугольник АВDE (рис. 2.1).
2) Строим вектор ![]() и перпендикулярно ему линии уровня, проходящие через
область.
и перпендикулярно ему линии уровня, проходящие через
область.
3) Из рисунка 2.1 видно, что
наиболее удаленной в направлении градиента угловой точкой является точка D, так как через нее проходит
самая дальняя линия уровня ![]() . Следовательно в точке D целевая функция принимает наибольшее значение, т.е.
. Следовательно в точке D целевая функция принимает наибольшее значение, т.е. ![]() . Через угловую точке А проходит ближайшая линия уровня
. Через угловую точке А проходит ближайшая линия уровня ![]() , следовательно, функция в точке А принимает наименьшее значение, т.е.
, следовательно, функция в точке А принимает наименьшее значение, т.е. ![]() .
.
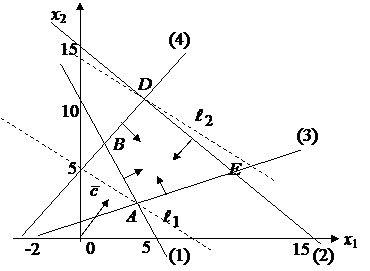
Рис. 2.1
Чтобы найти координаты точек А и D, нужно решить систему из уравнений тех прямых, на пересечении которых
лежат эти точки.
Точка А лежит на пересечении первой и третьей прямых.
Решим систему, составленную
из уравнений этих прямых
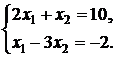
Получим ![]()
Точка D лежит на пересечении второй
и четвертой прямых.
Решим систему, составленную
из уравнений этих прямых
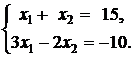
Получим ![]()
Пример 2. Найти наибольшее значение
функции ![]() при
ограничениях:
при
ограничениях:
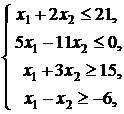
![]()
Решение.
1)
Строим область допустимых решений. Получим пятиугольник АВDEК
(рис. 2.2).
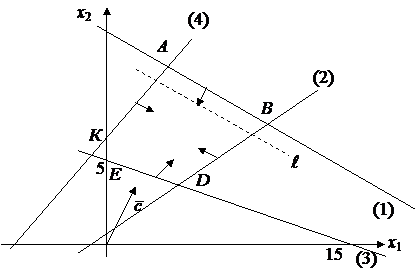
Рис.
2.2
2) Строим вектор ![]() и перпендикулярно ему линию уровня
и перпендикулярно ему линию уровня ![]() .
.
3) В данном случае линии
уровня параллельны прямой, проходящей через точки А и В.
Наибольшее значение целевая
функция принимает в любой точке отрезка АВ
(случай альтернативного оптимума). Найдем координаты точек А и В.
Точка А лежит на пересечении первой и четвертой прямых.
Решим систему, составленную
из уравнений этих прямых
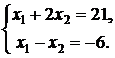
Получим ![]()
![]()
Точка В лежит на пересечении
первой и второй прямых.
Решая систему, составленную из
уравнений этих прямых, получим
![]()
Так как целевая функция
принимает наибольшее значение в любой точке отрезка АВ, то
![]() где
где ![]() или
или
![]()
Пример 3. Найти наибольшее значение
функции ![]() при
ограничениях:
при
ограничениях:
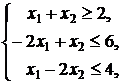
![]()
Решение.
1)  Строим область допустимых
решений.
Строим область допустимых
решений.
х1
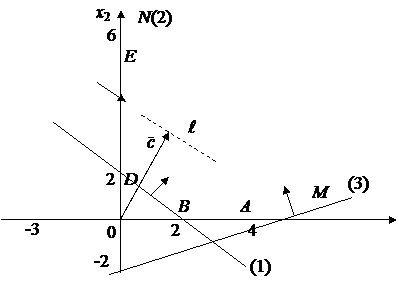
Рис.
2.3
OДP
представляет собой выпуклую неограниченную область MABDEN (рис. 2.3).
2) Строим вектор ![]() и линию уровня
и линию уровня ![]() , перпендикулярную к вектору
, перпендикулярную к вектору ![]() .
.
3) Так как в направлении вектора
![]() можно провести
сколь угодно удаленную линию уровня, проходящую через OДP, следовательно, функция в
этой области не достигает своего наибольшего значения
можно провести
сколь угодно удаленную линию уровня, проходящую через OДP, следовательно, функция в
этой области не достигает своего наибольшего значения
![]() .
.
Пример 4. Найти наибольшее значение
функции ![]() при ограничениях:
при ограничениях:
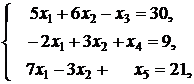
![]()
Решение. Выразим базисные переменные через свободные:
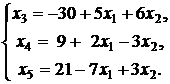
Исключим базисные переменные из целевой
функции, для этого в целевую функцию вместо базисных переменных подставим
их выражения через свободные переменные.
Получим: ![]()
Так как ![]() и
и ![]() то получим
систему неравенств
то получим
систему неравенств
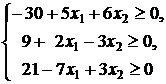 или
или 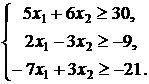
Исходная задача сведена к новой,
которую можно решить графически.
![]() ,
,
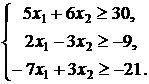
![]()
Решая эту задачу графически,
получим ![]()
Найдем оптимальное решение
исходной задачи, для этого найдем значения базисных переменных при ![]() и
и ![]() .
.
Тогда ![]() ;
; ![]()
![]()
Задачи
1. ![]()
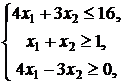
![]()
2. ![]()
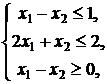
![]()
3. ![]()
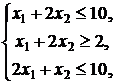
![]()
4. ![]()
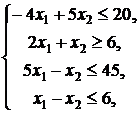
![]()
5. ![]()
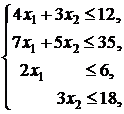
![]()
6. ![]()
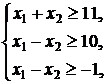
![]()
7. ![]()
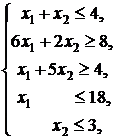
![]()
8. ![]()
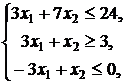
![]()
9. ![]()
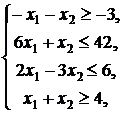
![]()
10. ![]()
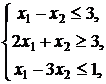
![]()
Ответы
1. 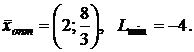
2. 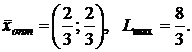
3. 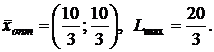
4. 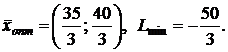
5. 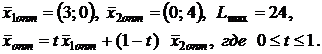
6. 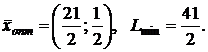
7. 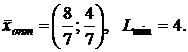
8. ![]()
9. Оптимального решения нет
из-за несовместности системы ограничений.
10.