Семинар 5. . Задачи на безусловный экстремум

В основе методов решения классических задач оптимизации лежит теория дифференциального исчисления.

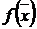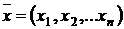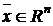Пусть - действительная дважды непрерывно дифференцируемая функция аргумента , . Требуется найти наибольшее (или наименьшее) значение данной функции и такое значение аргумента (оптимальное решение), при котором этот экстремум достигается.

Если точка является точкой экстремума функции, то она является стационарной точкой функции, т.е. частные производные в этой точке равны нулю:

, .

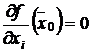Таким образом, экстремумы функции следует искать среди ее стационарных точек. Однако, возможно, не каждая стационарная точка является точкой экстремума.

Для решения вопроса о наличии экстремума функции многих переменных в стационарной точке находят значения вторых частных производных в этой точке и из полученных чисел составляют матрицу, называемую матрицей Гессе:

.

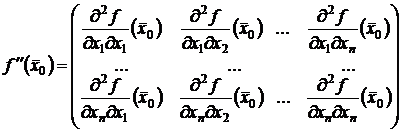Для того чтобы функция имела в стационарной точке локальный минимум, необходимо и достаточно, чтобы в этой точке все главные диагональные миноры матрицы Гессе были положительны.

Для того чтобы функция имела в стационарной точке локальный максимум, необходимо и достаточно, чтобы у матрицы Гессе главные диагональные миноры нечетных степеней были отрицательны в этой точке, а миноры четных степеней - положительны.

Пример 1. Исследовать на экстремум функцию

.

Решение. Найдем стационарные точки функции из условий

, .

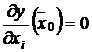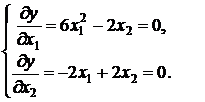
Данная система имеет два решения

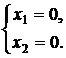или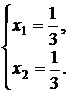

Найдены две стационарные точки: А(0;0) и В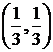. Проверим, являются ли они точками экстремума. Составим матрицу Гессе и вычислим ее значение в точке А.

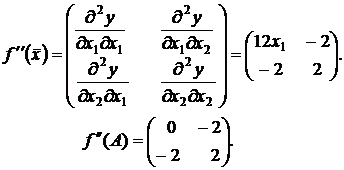
Вычислим главные диагональные миноры матрицы

М₁=0;

М₂=.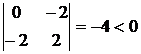

Следовательно, точка А не является точкой экстремума функции.

Составим матрицу Гессе в точке В:

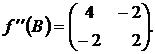
Вычислим главные диагональные миноры матрицы

М₁=4>0;

М₂=.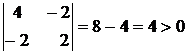

Следовательно, точка В является точкой минимума функции,

, .

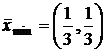Пример 2. Исследовать на экстремум функцию

.

Решение. Найдем стационарную точку из условий

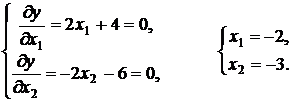
Итак, .

Исследуем статус этой точки, т.е. проверим, является ли она точкой экстремума. Для этого вычислим матрицу Гессе:

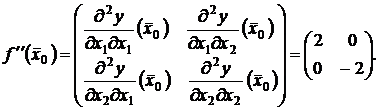
Вычислим главные диагональные миноры матрицы Гессе.

М₁=2

М₂=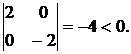

Минор второго порядка отрицателен, значит, в точке экстремума нет.

Задачи

Найти экстремумы функции:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10. .

Ответы

1. .

2. .

3. .

4. Экстремума нет.

5. .

6. .

7. .

8. .

9. .

10. .