Семинар 4. . Градиент функции многих переменных. Экстремумы.

Производная по направлению. градиент

Пусть функция определена в некоторой окрестности точки ; - некоторое направление, задаваемое единичным вектором , где - косинусы углов, образуемых вектором с осями координат, называемые направляющими косинусами.

При перемещении из точки в данном направлении в точку функция получает приращение , называемое приращением функции в данном направлении .

Пусть - величина перемещения.

Определение 1. Предел отношения при , если он существует, называется производной функции в точке по направлению и обозначается . Таким образом:

.

Производная характеризует изменения функции в направлении . При заданных направляющих косинусах производная по направлению вычисляется по формуле

.

Определение 2. Градиентом функции в точке называется вектор, координаты которого равны соответствующим частным производным и , взятым в точке и обозначается .

Таким образом:

,

или в координатной форме:

.

Пример 1. Вычислить производную функции в точке по направлению вектора , где - точка с координатами .

Решение. Найдем единичный вектор , имеющий данное направление.

. Его длина .

Следовательно, , .

Вычислим частные производные функции в точке .

.

.

Получим

.

Пример 2. Найти градиент функции в точке .

Решение. Находим частные производные в точке :

;

.

Получим

.

Экстремум функции двух переменных

Теорема 1. (необходимый признак существования экстремума). Если есть точка экстремума функции , то

в предположении, что указанные частные производные существуют в точке .

Заметим, что функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует.

Точки, в которых первые частные производные и функции обращаются в нуль или не существуют, называются критическими точками этой функции. Точки, в которых функция дифференцируема и частные производные равны нулю, называются стационарными.

Достаточным условием наличия экстремума в стационарной точке является условие

причем в случае точка есть точка максимума, а в случае - точка минимума.

Условие является достаточным условием отсутствия экстремума в стационарной точке .

В случае точка может быть, а может и не быть точкой экстремума (сомнительный случай). В этом случае необходимы дополнительные исследования.

Пример 3. Найти экстремумы функции

.

Решение. Находим первые частные производные:

и .

Приравняем найденные производные к нулю, после элементарных преобразований приходим к системе уравнений

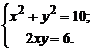
Решая данную систему уравнений, находим четыре стационарные точки:

.

Теперь найдем вторые частные производные:

и составим выражение

.

Убеждаемся, что:

1) - точка минимума;

2) в точке экстремума нет;

3) в точке экстремума нет;

4) - точка максимума.

Итак, данная функция имеет два экстремума: в точке - минимум , в точке - максимум .

Задачи

1) Найти градиент функции в точке .

Указание Найти , и найти градиент

Решение Находим частные производные в точке :

;

.

Получим.

Ответ .

2).Найти градиент функции в точке .

Указание Найти , и найти градиент

Решение Находим частные производные в точке :

;

.

Получим .

Ответ .

3). Найти экстремумы функции

.

Указание Найти частные производные первого и второго порядков и использовать признаки существования экстремумов

Решение Находим первые частные производные:

и .

Приравняем найденные производные к нулю, после элементарных преобразований приходим к системе уравнений

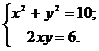
Решая данную систему уравнений, находим четыре стационарные точки:

.

Теперь найдем вторые частные производные:

и составим выражение

.

Убеждаемся, что:

1) - точка минимума;

2) в точке экстремума нет;

3) в точке экстремума нет;

4) - точка максимума.

Итак, данная функция имеет два экстремума: в точке - минимум , в точке - максимум .

Ответ В точке - минимум , в точке - максимум .