Семинар 3. . Функции многих переменных

Рассмотрим функцию двух переменных .

Зафиксируем значение одного из ее аргументов, например , положив . Тогда функция есть функция одной переменной .

Пусть она имеет производную в точке :

.

Данная производная называется частной производной (или частной производной первого порядка) функции по в точке и обозначается одним из следующих символов: ; ; ; .

Разность называется частным приращением по функции в точке и обозначается символом :

.

Учитывая приведенные обозначения, можно записать

.

Аналогично определяются и обозначаются частное приращение функции по и частная производная по в точке :

,

.

Значение частной производной зависит от точки , в которой она вычисляется. Поэтому частная производная функции двух переменных , вообще говоря, есть функция точки , т.е. также является функцией двух переменных и .

Все правила и формулы дифференцирования, выведенные для производных функций одной переменной, сохраняются для частных производных функции двух переменных.

Однако следует помнить, что при нахождении частной производной по какому-либо аргументу второй аргумент считается постоянным.

Пример 1. Найти частные производные функции

.

Решение. Частную производную находим как производную функции по аргументу в предположении, что .

Поэтому .

Аналогично .

Пример 2. .

Найти .

Решение.

.

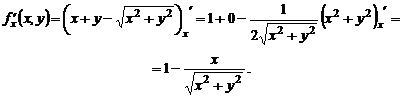Тогда .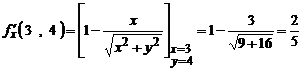

Задачи

1).Найти частные производные функции

.

Указание Частную производную находить как производную функции по аргументу в предположении, что . Частную производную находить как производную функции по аргументу в предположении, что .

Решение Частную производную находим как производную функции по аргументу в предположении, что .

Поэтому .

Аналогично .

Ответ ; .

2).Найти частные производные функции

.

Указание Частную производную находить как производную функции по аргументу в предположении, что . Частную производную находить как производную функции по аргументу в предположении, что .

Решение Частную производную находим как производную функции по аргументу в предположении, что .

Поэтому .

Аналогично .

Ответ ;

3).. Найти .

Указание Частную производную находить как производную функции по аргументу в предположении, что .

Решение Частную производную находим как производную функции по аргументу в предположении, что . Поэтому

.

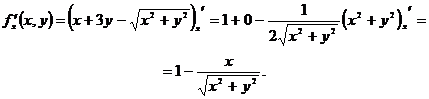Тогда .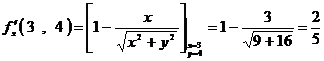

Ответ .

4). Найти полный дифференциал функции .

Указание Найти , и применить формулу полного дифференциала.

Решение Находим вначале и .

.

.

Тогда получим.

Ответ .

5).Найти полный дифференциал функции .

Указание Найти , и применить формулу полного дифференциала.

Решение Находим вначале и .

.

.

Тогда получим

.

Ответ .

6).Вычислить производную функции в точке по направлению вектора , где - точка с координатами .

Указание Найти , и применить формулу производной по направлению

Решение Найдем единичный вектор , имеющий данное направление.

. Его длина .

Следовательно, , .

Вычислим частные производные функции в точке .

.

.

Получим

.

Ответ .

7).Вычислить производную функции в точке по направлению вектора , где - точка с координатами .

Указание Найти , и применить формулу производной по направлению

Решение Найдем единичный вектор , имеющий данное направление.

. Его длина .

Следовательно, , .

Вычислим частные производные функции в точке .

.

.

Получим

.

Ответ .