Семинар 2. Системы линейных уравнений.

1). Решить систему линейных уравнений по формулам Крамера:

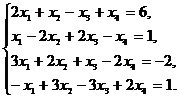
Указание Следует вычислить определитель системы. Если определитель отличен от нуля, то система имеет единственное решение, определяемое формулами Крамера.

Решение: Составим и вычислим главный определитель системы:

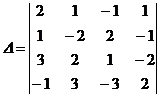
Создадим нули во втором столбце, для чего третий столбец прибавим ко второму, получим

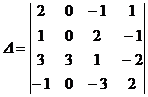
и разложим полученный определитель по элементам второго столбца.

,

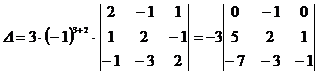здесь для получения нулей в первой строке элементы второго столбца, умноженные на 2, прибавили к первому столбцу и второй столбец прибавили к третьему, теперь определитель третьего порядка разложим по первой строке, получаем

Так как , то система имеет единственное решение. Составим определитель , заменив в первый столбец столбцом свободных членов, и вычислим его.

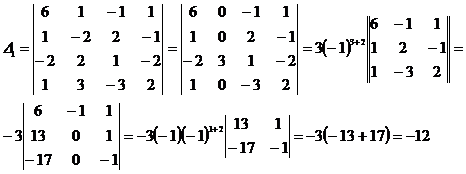
Находим определители .

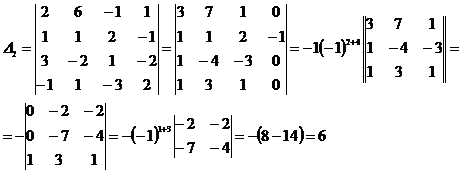
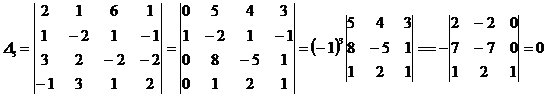
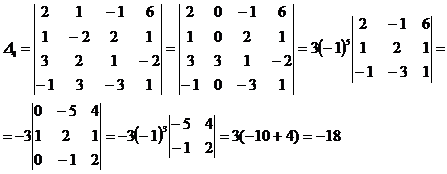
Ответ:

2). Решить систему линейных уравнений

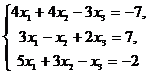
с помощью обратной матрицы (обратную матрицу найти с помощью элементарных преобразований).

Указание. Следует найти обратную матрицу для матрицы системы и умножить обратную матрицу на столбец свободных членов.

Решение Составим матрицу системы уравнений

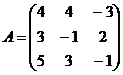
Будем искать обратную матрицу с помощью элементарных преобразований только над строками, для этого рядом с матрицей А через разделительную черту приписываем единичную матрицу того же порядка

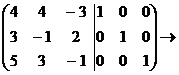
Создадим нули во втором столбце. Вторую строку оставим без изменения. Вторую строку, умноженную на4, прибавим к первой; вторую строку, умноженную на 3, прибавим к третьей:

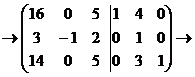
Теперь получим нули в третьем столбце. Третья строка остается без изменения. Третья строка, умноженная на -1, прибавляется к первой; вторая строка умножается на5:

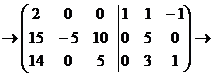
Теперь третью строку, умноженную на -2, прибавим ко второй и получим нули в третьем столбце:

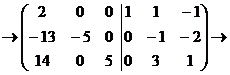
Вторую строку умножим на 2:

.

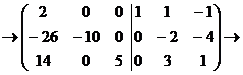Первую строку, умноженную на 13, прибавим ко второй, первую строку, умноженную на -7, прибавим к третьей:

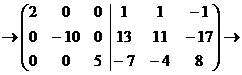
Первую строку умножим на 5, вторую на -1, третью на2, чтобы слева образовалась диагональная матрица с числом 10 на главной диагонали:

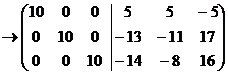
Обратная к матрице А имеет вид

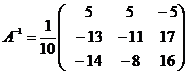
Решение системы уравнений ищем по формуле X=A^-1B, где Х-матрица-столбец неизвестных, В – матрица-столбец свободных членов системы.

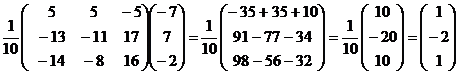
Ответ:

3). Найти общее и базисное решения системы линейных уравнений:

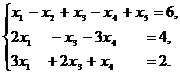
Указание. Для нахождения базисного решения запишите коэффициенты при неизвестных и свободные члены уравнений в виде таблицы. Используя обобщенный метод Гаусса, с помощью элементарных преобразований выполните исключение неизвестных, чтобы в каждом уравнении присутствовала неизвестная, исключенная из остальных уравнений системы.

Исключенные неизвестные образуют базис. Выразите базисные переменные через свободные и запишите общее решение. Придайте свободным переменным нулевые значения и выпишите базисное решение.

Решение.

Базис
x5	1 2 3	-1 0 0	1 -1 2	-1 -3 1	1 0 0	6 4 2
x5 x4	4 11 3	-1 0 0	3 5 2	0 0 1	1 0 0	8 10 2
x5 x4	4 2,2 3	-1 0 0	3 1 21	0 0 1	1 0 0	8 2 2
x5 x3 x4	-2,6 2,2 -1,4	-1 0 0	0 1 0	0 0 1	1 0 0	2 2 -2

Базисное решение: .

Общее решение: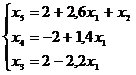

Ответ: Базисное решение: .

Общее решение: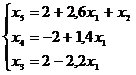

4). Найти общее и два базисных решения системы линейных уравнений:

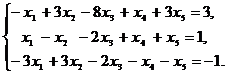
Указание. Для нахождения базисного решения запишите коэффициенты при неизвестных и свободные члены уравнений в виде таблицы. Используя обобщенный метод Гаусса, с помощью элементарных преобразований выполните исключение неизвестных, чтобы в каждом уравнении присутствовала неизвестная, исключенная из остальных уравнений системы.

Исключенные неизвестные образуют базис. Выразите базисные переменные через свободные и запишите общее решение. Придайте свободным переменным нулевые значения и выпишите базисное решение.

Решение.

Базис
	-1 1 -3	3 -1 3	-8 -2 -2	1 1 -1	3 1 -1	3 1 -1
x1	0 1 0	2 -1 0	-10 -2 -8	2 1 2	4 1 2	4 1 2
x2 x1	0 1 0	1 0 0	-5 -7 -8	1 2 2	2 3 2	2 3 2
x2 x1 x4	0 1 0	1 0 0	-1 1 -4	0 0 1	1 1 1	1 1 1
x2 x3 x4	1 1 4	1 0 0	0 1 0	0 0 1	2 1 5	2 1 5

Базисные решения: ,

Общее решение: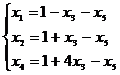

Ответ: Базисное решение: ,

Общее решение: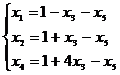

5). Найти общее и два базисных решения системы линейных уравнений:

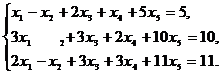
Указание. Для нахождения базисного решения запишите коэффициенты при неизвестных и свободные члены уравнений в виде таблицы. Используя обобщенный метод Гаусса, с помощью элементарных преобразований выполните исключение неизвестных, чтобы в каждом уравнении системы присутствовала неизвестная, исключенная из остальных уравнений.

Исключенные неизвестные образуют базис. Выразите базисные переменные через свободные и запишите общее решение. Придайте свободным переменным нулевые значения и выпишите базисное решение.

Решение.

Базис
	1 3 2	-1 0 -1	2 3 3	1 2 3	5 10 11	5 10 11
x2	-1 3 1	1 0 0	-2 3 1	-1 2 2	-5 10 6	-5 10 6
x2 x3	1 0 1	1 0 0	0 0 1	3 -4 2	7 -8 6	7 -8 6
x2 x3	1 0 1	1 0 0	0 0 1	3 1 2	7 2 6	7 2 6
x2 x4 x3	1 0 1	1 0 0	0 0 1	0 1 0	1 2 2	1 2 2
x1 x4 x3	1 0 0	1 0 -1	0 0 1	0 1 0	1 2 1	1 2 1

Базисные решения: ,

Общее решение: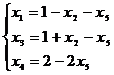

Ответ: Базисные решения: ,

Общее решение: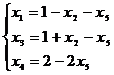

6). Найдите два опорных решения системы:

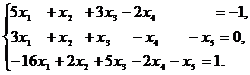
Указание. Используйте алгоритм нахождения базисных решений системы. При выборе ключевого элемента обратите внимание на требование минимальности отношения свободного члена уравнения к коэффициенту при выбранной переменной среди уравнений с положительными коэффициентами при выбранной переменной.

Решение.

Базис
	5 3 -16	1 1 2	3 1 5	-2 -1 -2	0 -1 -1	-1 0 1
	-5 3 -16	-1 1 2	-3 1 5	2 -1 -2	0 -1 -1	1 0 1
x2	-2 3 -22	0 1 0	-2 1 3	1 -1 0	-1 -1 1	1 0 1
x2 x5	-24 -19 -22	0 1 0	1 4 3	1 -1 0	0 0 1	2 1 1
x4 x2	-24 -43 -22	0 1 0	1 5 3	1 0 0	0 0 1	2 3 1
x4 x2 x3	-50/3 -19/3 -22/3	0 1 0	0 0 1	1 0 0	-1/3 -5/3 1/3	5/3 4/3 1/3

Ответ. , .

7). Найдите два опорных решения системы:

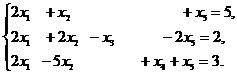
Указание. Используйте алгоритм нахождения базисных решений системы. При выборе ключевого элемента обратите внимание на требование минимальности отношения свободного члена уравнения к коэффициенту при выбранной переменной среди уравнений с положительными коэффициентами при выбранной переменной.

Решение.

Базис
x4	2 2 2	1 2 -5	0 -1 0	0 0 1	1 -2 1	5 2 3
x2 x4	1 1 7	0 1 0	1/2 -1/2 -5/2	0 0 1	2 -1 -4	4 1 8
x3 x2 x4	2 2 12	0 1 0	1 0 0	0 0 1	4 1 6	8 5 28
x2 x4	1/2 2 12	0 1 0	1/4 0 0	0 0 1	1 1 6	2 5 28
x5 x2 x4	1/2 3/2 9	0 1 0	1/4 -1/4 -3/2	0 0 1	1 0 0	2 3 16

Ответ. , .

7). Найдите два опорных решения системы:

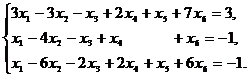
Указание. Используйте алгоритм нахождения базисных решений системы. При выборе ключевого элемента обратите внимание на требование минимальности отношения свободного члена уравнения к коэффициенту при выбранной переменной среди уравнений с положительными коэффициентами при выбранной переменной.

Решение.

Базис
	3 1 1	-3 -4 -6	-1 -1 -2	2 1 2	1 0 1	7 1 6	3 -1 -1
	3 -1 -1	-3 4 6	-1 1 2	2 -1 -2	1 0 -1	7 -1 -6	3 1 1
x5	3 -1 2	-3 4 3	-1 1 1	2 -1 0	1 0 0	7 -1 1	3 1 4
x5 x3	2 -1 3	1 4 -1	0 1 0	1 -1 1	1 0 0	6 -1 2	4 1 3
x5 x3 x4	-1 2 3	2 3 -1	0 1 0	0 0 1	1 0 0	4 1 2	1 4 3
x2 x3 x4	-0,5 3,5 2,5	1 0 0	0 1 0	0 0 1	0,5 -1,5 0,5	2 -5 4	0,5 2,5 3,5

Ответ. , .