Семинар 1. Вектора. Матрицы. Определители.

1). Вычислить определитель третьего порядка.

.

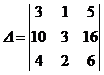Указание. Для вычисления определителя следует создать нули в какой-либо строке или столбце с использованием свойств определителей, чтобы затем разложить определитель по выбранной строке или столбцу.

Решение. Третья строка определителя содержит общий множитель 2, который можно вынести за знак определителя.

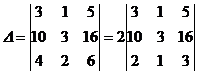
Будем вычислять определитель разложением по элементам третьей строки, предварительно создав в этой строке два нуля. Для этого второй столбец, умноженный на -2, прибавим к первому и второй столбец, умноженный на -3, прибавим к третьему, получаем

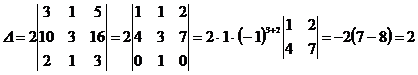
Ответ: 2.

2).Найти обратную к матрице

Указание . Нужно найти определитель матрицы. Если этот определитель отличен от нуля, то матрица невырожденная и можно найти обратную с помощью алгебраических дополнений. Если определитель матрицы равен нулю, то матрица не имеет обратной.

Решение. Найдем определитель матрицы .

Следовательно, матрица А невырожденная, поэтому для нее существует обратная . Найдем алгебраические дополнения для всех элементов матрицы А:

Составляем присоединенную матрицу, записывая алгебраические дополнения каждой строки в соответствующий по номеру столбец

.

Обратите внимание, как составляем присоединенную матрицу для квадратной матрицы второго порядка: элементы главной диагонали меняем местами, элементы побочной диагонали умножаем на -1.

Находим обратную матрицу:

.

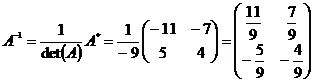Ответ: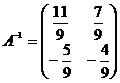

3). Показать, что система векторов образует базис трехмерного пространства и разложить вектор по этому базису.

Указание. Следует показать, что три вектора являются линейно независимыми. Тогда они образуют базис трехмерного пространства. Для этого находят ранг системы векторов, который должен совпасть с количеством векторов в системе, т.е. быть равным 3. Затем записывают разложение вектора по векторам базиса с неизвестными коэффициентами и решают систему линейных уравнений для отыскания неизвестных координат вектора в заданном базисе.

Решение. Составим матрицу координат векторов и найдем ранг.

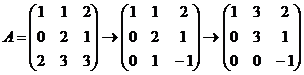
Здесь сначала первую строку, умноженную на -2, прибавили к третьей, затем поменяли местами второй и третий столбцы и наконец третий столбец, прибавили ко второму. Ранг матрицы и системы векторов равен 3. Следовательно, система векторов линейно независима и образует базис трехмерного пространства.

Представим вектор как линейную комбинацию базисных векторов с неизвестными координатами

Запишем это уравнение в координатной форме:

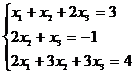
Эту систему решим методом исключения неизвестных.

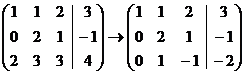
Здесь первую строку, умноженную на -2, прибавили к первой. Теперь третью строку прибавим ко второй, третью строку, умноженную на 2, прибавим к первой, затем третью строку умножим на -1.

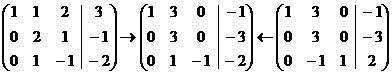
Далее вторую строку, умноженную на -1, прибавим к первой, вторую строку разделим на 3, вторую строку прибавим к третьей.

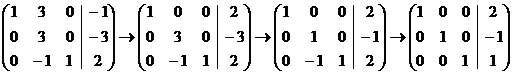
Получено решение системы уравнений:

Разложение вектора по базису принимает вид:

Ответ: