Лекция 9. Межотраслевой баланс

Межотраслевой баланс (МОБ) представляет собой инструмент анализа и прогнозирования структурных взаимосвязей в экономике. Метод его построения состоит в двойственном рассмотрении различных отраслей и секторов экономики: с одной стороны, как потребляющих продукцию, с другой - как выпускающих те или иные виды товаров и услуг для собственного потребления и нужд других отраслей экономики.

Межотраслевой баланс - это "шахматная таблица" отраслей, в которой по вертикали показываются материальные затраты на производство продукции определенной отрасли хозяйства, по горизонтали - количество продукции, переданное из данной отрасли в другие на производственные нужды (промежуточный продукт), а также конечное потребление продукции отраслью. Используя эти данные, можно определить удельные затраты какого-либо ресурса на выпуск конечного продукта. Для этого выбранный показатель столбца или строки делится на величину валового продукта. Например, разделив величину затрат электроэнергии на объем продукции машиностроения, получим удельное электропотребление машиностроительного производства.

В мировую экономику эта модель вошла из публикаций Василия Васильевича Леонтьева, известного американского экономиста русского происхождения. В. Леонтьев создал научно обоснованный метод "затраты-выпуск", который позволяет анализировать межотраслевые связи в национальном хозяйстве и определять возможные направления оптимизации отраслевой структуры. За это научное достижение ему была присуждена Нобелевская премия.

Межотраслевой баланс.

Структура и содержание таблицы межотраслевого баланса

Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе.

Балансы бывают отчетные и плановые. Отчетные фиксируют сложившиеся пропорции, а плановые отражают некоторое желательное состояние и получаются в результате расчета по моделям, о которых и пойдет речь в этой главе.

В зависимости от того, в каких единицах измеряются межотраслевые потоки, различают балансы натуральные и стоимостные. Далее мы будем иметь в виду в основном стоимостные балансы.

Предположим, что народное хозяйство представлено совокупностью п отраслей. Будем считать, что каждая отрасль производит только один продукт и каждый продукт производится только одной отраслью, т.е. между отраслями и продукцией существует взаимно однозначное соответствие. В действительности это не так, поэтому в МОБ фигурируют не реальные, а так называемые «чистые», или «технологические», отрасли.

Общий вид межотраслевого баланса представлен в табл.1. Она состоит из четырех разделов. Первый раздел образуется перечнем «чистых» отраслей. Каждая отрасль представлена в МОБ дважды: как производящая и как потребляющая. Отрасли как производителю соответствует строка таблицы, отрасли как потребителю соответствует столбец. На пересечении i-й строки и j-го столбца находится величина x_ij — количество продукции i-й отрасли (в денежном выражении), израсходованной на производственные нужды j-й отрасли. Таким образом, первый раздел характеризует межотраслевые потоки сырья, материалов, энергии и т.д., обусловленные производственной деятельностью отраслей. По данным этого квадрата вычисляют коэффициенты прямых и полных затрат, на производство продукции.

Таблица 1 Общий вид межотраслевого баланса

	1	2	…	n	У	Х
1	x11	x12	…	x1n	y1	x1
2	х21	x22		x2n	y2	x2
…	…	…	…	…	…	…
n	xn1	xn2	…	xnn	yn	xn
V	v 1	v2	…	vn
Х	x1	x2	. . .	xn

Второй раздел МОБ состоит из двух столбцов. Столбец Y — это конечная продукция отраслей. Конечная продукция включает в себя непроизводственное потребление (личное и общественное), возмещение выбытия основных фондов и накопление. Накопление делится на производственные основные фонды, непроизводственные основные фонды, прирост оборотных фондов, увеличение запасов и резервов. Столбец Х содержит величины валового производства отраслей. В целом данные второго квадрата характеризуют отраслевую материальную структуру дохода, его состав, показывают распределение дохода на фонд накопления и потребления, а также структуру накопления и потребления по отраслям производства и потребителям.

Третий раздел представлен двумя нижними строками. Строка Х содержит те же самые величины, что и соответствующий столбец второго раздела. Строка V содержит величины условно-чистой продукции отраслей. Условно-чистая продукция включает в себя амортизационные отчисления и вновь созданную стоимость (заработную плату и прибыль).

Четвертый раздел МОБ не имеет непосредственного отношения к анализу межотраслевых связей. Он характеризует перераспределительные отношения в народном хозяйстве и здесь рассматриваться не будет.

Натуральные балансы содержат перечень не отраслей, а самих продуктов материального производства – уголь, сталь, нефть, зерно, мясо и т.д. В качестве единиц измерения выступают специфические для каждого продукта количественные характеристики – вес, объем, площадь, длина и т.д. В натуральном балансе первый и второй квадраты по содержанию аналогичны стоимостным. Каждая строка представляет собой материальный баланс отдельного продукта. В третьем квадрате отражаются затраты в натуральном измерении, на производство каждого вида продукции. Суммирование по столбцам в натуральном балансе не производится и стоимостная структура не выявляется. Основное значение межпродуктового баланса заключается в комплексном, математически взаимосвязанном рассмотрении материальных балансов важнейших видов продукции.

Строки стоимостных балансов показывают распределение продукции. Для любой i-й строки первого раздела справедливо соотношение

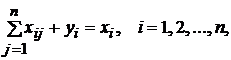(1)

т.е. вся произведенная i-й отраслью продукция хi (валовая продукция в денежном выражении) делится на промежуточную и конечную. Промежуточная продукция — это та часть валовой продукции i-й отрасли, которая расходуется другими отраслями в процессе осуществления ими собственных производственных функций.

Столбцы МОБ показывают структуру затрат. Для любого j-го столбца можно записать:

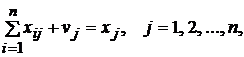(2)

т.е. стоимость всей произведенной j-й отраслью продукции х_j состоит из текущих производственных затрат и условно-чистой продукции v_j.

Суммарный конечный продукт равен суммарной условно-чистой продукции. Действительно,

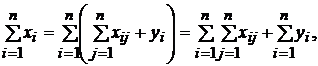(3)

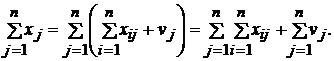(4)

Сравнивая правые части соотношений (3) и (4), видим, что

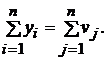
Зная суммарный конечный продукт, или суммарную условно-чистую продукцию, можно определить национальный доход. Он равен разности суммарного конечного продукта и амортизационных отчислений, направляемых на возмещение выбытия основных фондов.

Модель Леонтьева. Коэффициенты прямых и полных материальных затрат

Рассмотренная таблица МОБ всего лишь форма представления статистической информации о взаимосвязи отраслей. Перейдем теперь к построению математической модели. Для этого введем понятие коэффициентов прямых материальных затрат:

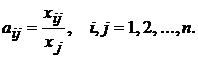(5)

Коэффициент a_ij показывает, какое количество i-го продукта затрачивается на производство единицы j-го продукта.

Поскольку продукция измеряется в стоимостных единицах, коэффициенты прямых затрат являются величинами безразмерными. Кроме того, из (5) следует, что

(6)

Считая коэффициенты прямых материальных затрат постоянными, запишем систему балансовых соотношений (1) следующим образом:

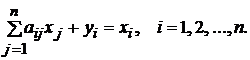
Перенося y_i в правую часть, а x_i в левую и меняя знаки на противоположные, получаем

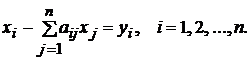(7)

В матричной форме эта система уравнений выглядит следующим образом:

X – AX = Y или (E – A) X = Y, (8)

где Е — единичная матрица n-го порядка; A — матрица коэффициентов прямых материальных затрат.

Итак, мы получили систему уравнений межотраслевого баланса, которую называют моделью Леонтьева. Используя эту модель, можно ответить на основной вопрос межотраслевого анализа — каким должно быть валовое производство каждой отрасли для того, чтобы экономическая система в целом произвела заданное количество конечной продукции?

Следует отметить одно важное свойство матрицы А — сумма элементов любого ее столбца меньше единицы:

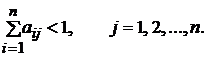(9)

Для доказательства разделим обе части балансового соотношения (2) на х_j и, выполнив простейшие преобразования, получим

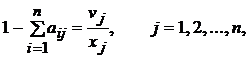
где v_j / x_j= — доля условно-чистой продукции в единице валового выпуска.

Очевидно, что >0, так как в процессе производства не может не создаваться новой стоимости. Из этого следует справедливость соотношения (9).

Свойства (6) и (9) матрицы А играют ключевую роль в доказательстве ее продуктивности, т.е. в доказательстве того, что при любом неотрицательном Y система (8) имеет единственное и неотрицательное решение Х=(Е–А)^-1 Y. Матрицу (Е –А)^-1 обозначают через В и называют матрицей коэффициентов полных материальных затрат, или обратной матрицей Леонтьева. Элемент b_ij этой матрицы показывает, каким должен быть валовой выпуск i-й отрасли для того, чтобы обеспечить производство единицы конечного продукта j-й отрасли. Используя матрицу В, можем записать

Х = ВY (10)

или в развернутом виде

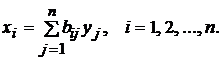(11)

Преимущество такой формы записи балансовой модели состоит в том, что, вычислив матрицу В лишь однажды, мы можем многократно использовать ее для вычисления Х прямым счетом, т.е. умножением В на Y. Это гораздо проще, чем каждый раз решать систему линейных уравнений.

Используя матрицу полных затрат В можно: провести анализ взаимосвязей для выпуска конечной и валовой продукции; определить полные затраты народного хозяйства для выпуска конечной продукции; оценить влияние на экономику изменений в структуре составляющих конечной продукции; рассчитать какое влияние окажет на народное хозяйство изменение коэффициентов прямых затрат; определить структуру основных фондов производственных отраслей, необходимую для выпуска данного объема конечной продукции.

Обратную матрицу В можно вычислить, используя метод обращения с применением формулы разложения ее в матричный ряд:

В=Е+А+А²+...+А^k+... (12)

Число членов ряда, необходимое для получения достаточно точного приближения, зависит от матрицы А, но в любом случае приемлемый результат достигается при k ³ 30.

Формула (12) имеет строгое математическое доказательство. Но мы ограничимся тем, что попытаемся осмыслить ее, рассматривая Х как результат некоторого гипотетического процесса последовательного уточнения промежуточной продукции, необходимой для создания заданного конечного продукта.

Итак, вектор конечной продукции, которую должна произвести экономическая система, равен Y. Будем считать, что это и есть первоначальное задание отраслям, т.е. Х₀= Y. Для выполнения собственного задания каждая отрасль нуждается в продукции других отраслей. Если бы все отрасли подсчитали потребности и подали заявки в некоторый центр, то оказалось бы, что суммарная потребность составляет X₁ = АХ₀ = АY. Вектор X₁ можно рассматривать как промежуточную продукцию, необходимую для производства Х₀. Но под обеспечение производства X₁ тоже нужна промежуточная продукция: X₂ = АХ₁ = А²Y. Рассуждая так и далее, мы приходим к выводу, что

Х = Х₀+Х₁+Х₂+...+Х_k+... = Y+АY+А²Y+...+A^kY+... =

= (E+A+A²+…+A^k+...)Y.

Полные затраты можно разложить на прямую и косвенную составляющие. Прямые затраты осуществляются непосредственно при производстве данного продукта, а косвенные А²+А³+…+А^k+... относятся к предшествующим стадиям производства. Они осуществляются не прямо, а через посредство других ингредиентов, входящих в данный продукт. Элементы матрицы А² представляют собой косвенные затраты первого порядка, элементы матрицы А³ — косвенные затраты второго порядка и т.д.

Пример 1. Рассматривается трехотраслевой МОБ. Известна матрица коэффициентов прямых материальных затрат и задан вектор конечного продукта:

.

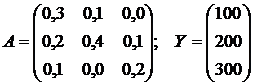Определить валовое производство X, обеспечивающее заданный конечный продукт.

Для ответа на поставленный вопрос необходимо составить и решить систему линейных уравнений (Е –А)Х = Y.

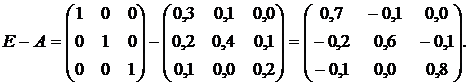
Получим соответствующую систему уравнений

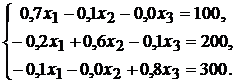
Решим систему методом Крамера. Если определитель системы отличен от нуля, то система имеет единственное решение, которое находится по формулам

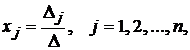
где Δ_j — определитель, который получается из Δ заменой j-го столбца столбцом свободных членов.

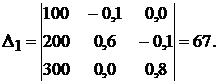
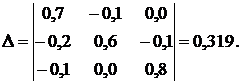
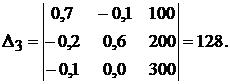
Применяя формулы Крамера, получаем решение системы:

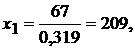
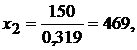
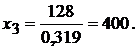
Пример 2. Вычислить изменение межотраслевых потоков, если известна матрица коэффициентов полных материальных затрат и задан вектор изменения конечного продукта:

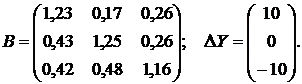
Изменение межотраслевых потоков вычисляется по формулам

Вектор изменения валового производства определяется следующим образом:

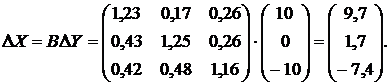
Кроме того, нам необходимо знать матрицу А. Из формулы В=(Е–А)^-1 следует, что

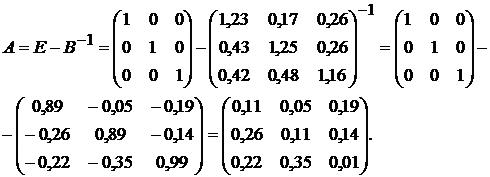
Теперь, отвечая на поставленный вопрос, получаем:

и т.д.

Показатели использования ресурсов. Прямая и полная трудоемкость и фондоемкость

К числу важнейших аналитических возможностей данного метода относится определение прямых и полных затрат труда на единицу продукции и разработка на этой основе балансовых продуктово-трудовых моделей, исходной моделью при этом служит отчетный межпродуктовый баланс в натуральном выражении. В этом балансе по строкам представлено распределение каждого отдельного продукта на производство других продуктов и конечное потребление (первый и второй квадранты схемы межотраслевого баланса). Отдельной строкой дается распределение затрат живого труда в производстве всех видов продукции; предполагается, что трудовые затраты выражены в единицах труда одинаковой степени сложности.

Обозначим затраты живого труда в производстве j-го продукта через L_j а объем производства этого продукта (валовой выпуск), как и раньше, через X_j Тогда прямые затраты труда на единицу j-го вида продукции (коэффициент прямой трудоемкости) можно задать следующей формулой:

Пусть L — среднегодовая численность работников i-й отрасли. По аналогии с коэффициентами прямых материальных затрат вводятся коэффициенты прямых затрат труда:

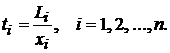(13)

Зная эти коэффициенты, можем вычислить суммарную потребность в трудовых ресурсах при заданном объеме валового производства:

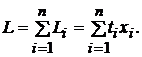
Валовое производство можно выразить через конечную продукцию по формуле (5.11). Воспользуемся этой формулой и запишем предыдущее соотношение так:

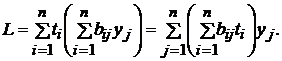
Величина b_ijt_i показывает, какое количество трудовых ресурсов i-й отрасли необходимо для того, чтобы обеспечить i-й продукцией выпуск единицы j-го конечного продукта. Суммируя эти величины по всем отраслям, получаем

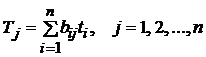(14)

или в векторной форме:

Т = В^Tt.

Т_j — коэффициент полных затрат труда (полная трудоемкость). Он показывает, какое количество трудовых ресурсов всех отраслей необходимо для производства единицы j-го конечного продукта.

Таким образом, суммарная потребность в трудовых ресурсах может быть вычислена двумя способами:

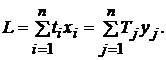(15)

Аналогично определяются коэффициенты прямой и полной фондоемкости. Пусть F_i — среднегодовое количество используемых основных фондов. Тогда коэффициент прямой фондоемкости

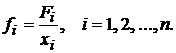(16)

Коэффициент полной фондоемкости

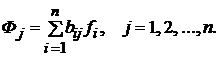(17)

То же в векторной форме:

Ф = В^Tt.

Коэффициент Ф_j показывает, какое количество основных фондов всех отраслей необходимо для производства единицы j-го конечного продукта.

По аналогии с (5.15) суммарная потребность в основных фондах вычисляется так:

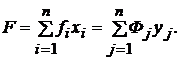(18)

Соотношение (18) представляет собой основное балансовое равенство в теории межотраслевого баланса труда. В данном случае его экономическое содержание заключается в том, что стоимость конечной продукции, оцененной по полным затратам труда, равна совокупным затратам живого труда. Сопоставляя потребительский эффект различных взаимозаменяемых продуктов с полными трудовыми затратами на их выпуск, можно судить о сравнительной эффективности их производства. С помощью показателей полной трудоемкости более полно и точно, чем при использовании существующих стоимостных показателей, выявляется структура затрат на выпуск различных видов продукции и прежде всего соотношение между затратами живого и овеществленного труда.

На основе коэффициентов прямой и полной трудоемкости могут быть разработаны межотраслевые и межпродуктовые балансы затрат труда и использования трудовых ресурсов. Схематически эти балансы строятся по общему типу матричных моделей, однако все показатели в них (межотраслевые связи, конечный продукт, условно чистая продукция и др.) выражены в трудовых измерителях.

Коэффициенты полной трудоемкости и фондоемкости можно подобно коэффициентам полных материальных затрат рассматривать как сумму прямой и косвенной составляющих. Например, для полной фондоемкости:

Ф = (Е+А+А²+...+А^к+...)^Тf = f+(А+А²+...+А^k+...)^Тf.

Косвенная составляющая полной фондоемкости (так же, как и полной трудоемкости) сравнительно невелика в сырьевых отраслях и возрастает в «завершающих» отраслях до 90 ¸ 95%.

Пример 3. Вычислить общую потребность в трудовых ресурсах, если известны коэффициенты прямых материальных затрат, коэффициенты прямых затрат труда и задан вектор конечного продукта:

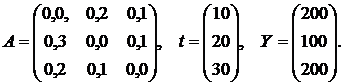
Для решения этой задачи нужно воспользоваться формулой

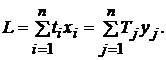
Как видим, возможны два способа:

1) вычислить Х = ВY, а затем применить формулу L = (t,x);

2) вычислить коэффициенты полных затрат труда Т = B^Tt и далее L = (Т,Y). Но в обоих случаях необходимо сначала вычислить

матрицу В.

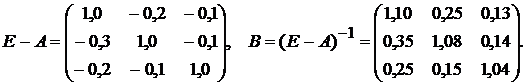
Первый способ:

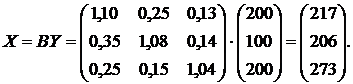
Второй способ:

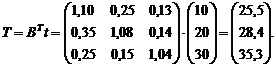
Пример 4. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

; ,

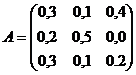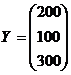а так же затраты живого труда (трудовые ресурсы) в трех отраслях: L₁=1160, L₂=460, L₃=875 в некоторых единицах измерения трудовых затрат. Требуется определить коэффициенты прямой и полной трудоемкости и составить межотраслевой баланс затрат труда.

Найдем матрицу коэффициентов полных материальных затрат для матрицы А:

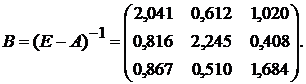
Валовая продукция (вектор X), тогда равна:

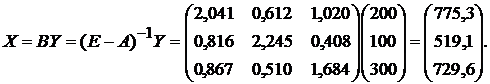
Воспользовавшись формулой (25), находим коэффициенты прямой трудоемкости:

Развитие основной модели межотраслевого баланса достигается также путем включения в нее показателей фондоемкости продукции. В простейшем случае модель дополняется отдельной строкой, в которой указаны в стоимостном выражении объемы производственных фондов Ф_j, занятые в каждой j-й отрасли. На основании этих данных и объемов валовой продукции всех отраслей определяются коэффициенты прямой фондоемкости продукции j- й отрасли:

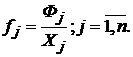(31)

Коэффициент прямой фондоемкости показывает величину производственных фондов, непосредственно занятых в производстве данной отрасли, в расчете на единицу ее валовой продукции. В отличие от этого показателя коэффициент полной фондоемкости F_j отражает объем фондов, необходимых во всех отраслях для выпуска единицы конечной продукции j-й отрасли. Если a_ij– коэффициент прямых материальных затрат, то для коэффициента полной фондоемкости справедливо равенство, аналогичное равенству (26) для коэффициента полной трудоемкости:

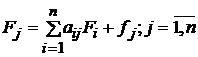. (31)

Если ввести в рассмотрение вектор-строку коэффициентов прямой фондоемкости f=(f₁, f₂, …f_n) и вектор-строку коэффициентов полной фондоемкости F=(F₁, F₂,…F_n), то систему уравнений (5.31) можно переписать в матричной форме:

F=FA+f_j. (32)

Для более глубокого анализа необходимо дифференцировать фонды на основные и оборотные, а в пределах основных – на здания, сооружения, производственное оборудование, транспортные средства и т.д.

Пусть в целом все производственные фонды разделены на t групп. Тогда характеристика занятых в народном хозяйстве фондов задается матрицей показателей Ф_kj , отражающих объем фондов k-й группы, занятых в j-й отрасли:

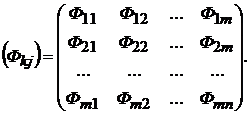
Коэффициенты прямой фондоемкости также образуют матрицу размерности , элементы которой определяют величину производственных фондов k-й группы, непосредственно используемых при производстве единицы продукции j- й отрасли:

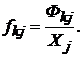
Для каждой j-й отрасли могут быть вычислены коэффициенты полной фондоемкости F_kj, отражающие полную потребность в фондах k-й группы для выпуска единицы конечной продукции этой отрасли:

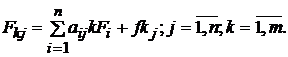
Решение системы данных уравнений позволяет представить коэффициенты полной фондоемкости по каждой из t групп фондов как функцию коэффициентов прямой фондоемкости:

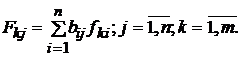
В этих формулах величины a_ij и b_ij – уже известные коэффициенты прямых и полных материальных затрат.

Коэффициенты фондоемкости в межотраслевом балансе позволяют увязать планируемый выпуск продукции с имеющимися производственными мощностями. Так, потребность в функционирующих фондах k-й группы для достижения заданного объема материального производства X_j по всем отраслям задается формулой 

Динамические модели.

Магистральная модель Дж. фон Неймана

Рассмотренные выше модели МОБ были статическими, т.е. относились к какому-то одному периоду времени. Динамическая модель отражает развитие экономической системы во времени и отличается от статической следующими чертами:

— содержит соотношения, определяющие зависимость последующих состояний от предыдущих;

— предусматривает дифференциацию конечного продукта каждого периода на две составляющие — непроизводственное потребление и накопление (инвестиции).

В динамических межотраслевых моделях капиталовложения в производство выделены из состава конечной продукции и рассматриваются как межотраслевые производственные потоки, обеспечивающие прирост фондов.

Существуют различные типы динамических моделей. Все они довольно сложны и различаются в основном по способу описания взаимосвязи инвестиций с динамикой объемов производства.

Особую группу составляют магистральные модели. Они позволяют рассчитывать оптимальные траектории экономического роста (магистрали). Критерии оптимальности, а также предпосылки и допущения, при которых формулируются модели, могут быть разными.

Рассмотрим магистральную модель равновесного роста, предложенную американским математиком Дж. фон Нейманом. Она называется равновесной потому, что моделирует процесс развития экономики в предположении, что пропорции потребления и инвестиций постоянны.

Будем рассматривать развитие экономической системы в дискретном времени (по годам).

Для года можно записать:

, (19)

где — вектор валового производства;

— соответствующий конечный продукт;

— вектор инвестиций;

— вектор потребления (выбытием основных фондов пренебрегаем).

Пусть известен вектор, определяющий сложившуюся структуру потребления. Будем считать его постоянным. Тогда

, (20)

где — суммарный конечный продукт.

Для определения можно воспользоваться тем, что суммарный конечный продукт равен суммарной условно-чистой продукции:

(21)

где — вектор относительной условно-чистой продукции. Его компоненты определяются по уже известной нам формуле

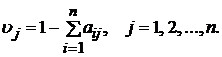
Объединяя формулы (5.20) и (5.21), получим соотношение, выражающее потребление как функцию валового производства:

(22)

где.

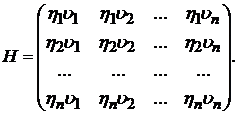
Рассмотрим теперь, какова связь между валовым производством и инвестициями. Очевидно, что инвестиционный спрос зависит от желаемого прироста валового производства:

где К — матрица коэффициентов капиталоемкости (приростной фондоемкости).

Она характеризует капитальные затраты, необходимые для наращивания производственного потенциала отраслей. Элемент этой матрицы показывает, какое количество продукции i-й отрасли необходимо для того, чтобы за счет наращивания фондов обеспечить единичный прирост производства в j-й отрасли.

Как было сказано выше, в модели предполагается стабильный, равновесный рост. Если темп роста обозначить через , то

Из этого следует, что

(23)

Итак, мы выразили две составляющие конечного продукта через валовое производство. Подставляя (22) и (23) в формулу (19), получаем

(24)

Заметим, что в этой модели индекс времени не играет никакой роли. Так получилось потому, что модель сформулирована в предположении, что ситуация в каждом следующем году структурно повторяет ситуацию предыдущего года.

Опуская индекс времени и осуществляя простейшие преобразования, из соотношения (24) получаем

Если предположить, что в матрице приростной фондоемкости отсутствуют нулевые строки (в общем случае это условие не выполняется, поскольку не все отрасли производят средства производства), то, умножив обе части последнего соотношения на , получаем

где

Таким образом, расчет параметров равновесного роста сводится к определению собственных значений и собственных векторов матрицы . В нашем случае множество собственных значений есть множество возможных темпов роста. Очевидно, нас интересует наибольший темп. Поэтому здесь необходимо решить не общую, а так называемую частную задачу, т.е. найти наибольшее собственное значение и соответствующий ему вектор X.

Как известно, собственные векторы находятся с точностью до постоянного множителя. Можно так подобрать этот множитель, что сумма компонентов вектора Х будет равна 1. В этом случае мы получим магистраль фон Неймана — пропорции валового производства, при которых обеспечивается сложившаяся структура потребления и достигается наибольший ежегодный экономический рост.

Модель фон Неймана формулируется при жестких условиях и предположениях, поэтому представляет собой сугубо абстрактное построение. Тем не менее она имеет важное значение, поскольку дает теоретическое обоснование того, что одним из условий интенсивного, устойчивого развития экономики является оптимизация пропорций валового производства.