Лекция 8. Производственные функции.

Производственные функции, их свойства.

Производственной функцией называется зависимость объема производства у от затрат производственных ресурсов . В общем виде эта зависимость представляет собой числовую собой функцию нескольких переменных

,

или , где – вектор факторов производства.

В другом варианте в число аргументов функции может быть включен вектор параметров . Присутствие этого вектора обусловлено возможностью учета случайной компоненты при математическом моделировании зависимости. В процессе параметризации выполняется оценка параметров модели, т.е. их расчет методами регрессионного анализа.

Производственные функции, или функции выпуска, предназначены для моделирования производства на макро- и микроэкономическом уровнях. Они используются для математического описания и исследования производства отдельной фирмы, производственного комплекса, отрасли, экономики региона, национальной экономики. С их помощью решаются задачи прогнозирования экономического роста, оценки эффективности ресурсов, планирования развития производства, оптимизации выпуска или издержек и т. д.

В зависимости от количества используемых в производстве ресурсов, производственные функции называют одно- или многофакторными. Количество ресурсов может быть представлено в натуральной или стоимостной форме. В теоретических исследованиях часто применяют двухфакторные производственные функции, поскольку они представляют собой геометрически иллюстрируемый наиболее простой вид многофакторных функций. При этом они отражают свойства взаимосвязей достаточно корректно. Введение большего количества переменных возможно, но это усложняет задачу параметризации модели и, соответственно, может привести к существенным погрешностям, ошибкам и техническим сложностям.

Среди прочих показателей в экономическом анализе часто используются средние и предельные величины. Средняя величина показателя вычисляется как отношение значения определяющей его функции к соответствующему значению аргумента. Для обозначения средних величин к обычному обозначению величин добавляется буква А. Например, для производственной функции, отношение

называется средней производительностью i-го фактора производства. Она показывает, сколько единиц выпускаемой продукции приходится на единицу затраченного ресурса.

Под предельным (маржинальным) значением величины принято понимать производную (частную производную) функции этой величины (если эта функция непрерывна). Для обозначения предельных величин к обычному обозначению добавляется буква М. Так, предельной (маржинальной) производительностью i-го фактора производства называют величину:

.

Она показывает приближенно, сколько дополнительных единиц продукции приносит дополнительно затраченная малая единица соответствующего ресурса (фактора). Если функция показателя дискретна, то под предельной (маржинальной) величиной понимают отношение изменения функции к вызвавшему это изменение приращению независимой переменной. Предельные величины выражают прирост соответствующего показателя в расчете на единицу прироста определяющего его фактора. Так, предельный продукт характеризует приближенно прирост производства при увеличении затрат ресурса на единицу.

Эластичностью непрерывной функции называется предел отношения относительного приращения функции к относительному приращению аргумента при стремлении приращения аргумента к нулю:

.

Эластичность может быть выражена в виде отношения предельной и средней величин:

.

Эластичность функции - безразмерная величина, значение которой не зависит от того, в каких единицах измерены величины x и y. Она показывает приближенно, на сколько процентов изменится функция при изменении аргумента на 1%.

Для того чтобы производственная функция являлась адекватной моделью производственного процесса, она должна обладать рядом свойств, характерных как для данного процесса, так и для экономических процессов в целом. В то же время, вид функции должен быть удобным для применения математических методов при исследовании и анализе. Желательно, чтобы функция была непрерывной. В итоге, построение производственных функций выполняется на основе следующих предпосылок.

1. Функция задана в области неотрицательных значений переменных:

.

2. При отсутствии хотя бы одного производственного ресурса производство невозможно:

;

.

3. Увеличение объема одного из ресурсов при неизменных объемах других ресурсов не уменьшает объем производства:

.

4. Увеличение затрат одного ресурса при неизменных объемах других ресурсов приводит к снижению прироста выпуска на каждую дополнительную единицу данного ресурса (убывающая эффективность ресурса):

.

5. С ростом одного ресурса (при неизменных количествах других) предельная эффективность другого ресурса не убывает:

.

При анализе функций двух переменных наглядное представление о форме поверхности могут дать линии уровня. Линии уровня производственной функции называются изоквантами. Семейство изоквант задается уравнением y = Const или , где С – параметр, фиксирующий объем производства на некотором уровне. Изокванты двухфакторной функции представляют собой семейство непересекающихся линий, в плоскости , образующих так называемую карту изоквант. Через каждую точку области определения проходит одна изокванта. Различные точки одной и той же изокванты задают различные комбинации ресурсов позволяющие произвести одинаковое количество продукции y = C.

При перемещении точки по линии уровня количество используемых производственных ресурсов меняется при фиксированном уровне производства y = C. Происходит замещение одного ресурса другим. Это означает, что единицу одного ресурса можно заменить некоторым количеством другого ресурса так, что объем продукции при этом останется прежним. Скажем, при определенной структуре производства добавление 1 чел./ч. труда дает такой же прирост продукции, как и увеличение на 2 ден./ед. производственных фондов. Для оценки скорости замещения используется понятие нормы замещения i-го ресурса j-м:

.

В частности, ; . Если приращение (очень незначительно), то оценкой скорости замещения одного товара другим становится предельная норма замещения i-го ресурса j-м:

.

Эта величина приближенно показывает, на сколько единиц необходимо увеличить затраты j-го ресурса, чтобы сохранить неизменным объем выпуска продукции при сокращении затрат i-го ресурса на единицу. Предельная норма замещения в любой точке изокванты может быть выражена через предельные производительности факторов (ресурсов) производства. Для всех точек, принадлежащих одной изокванте, изменение выпуска при приращении одного из ресурсов равно нулю. Математически это записывается как равенство нулю полного дифференциала производственной функции:

.

Тогда

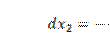, или .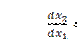

.

Некоторые виды двухфакторных производственных функций.

1. Линейная производственная функция:

.

Данный вид функциональной зависимости применяется для моделирования производственных процессов, в которых факторы производства могут полностью замещать друг друга, например, при описании макроэкономических систем. В случае, когда , для этой функции будет нарушено свойство нулевого выпуска при нулевом объеме ресурсов, изокванты могут пересекать координатные оси. Карта изоквант линейной функции представляет собой семейство отрезков параллельных прямых с отрицательным угловым коэффициентом (рис.1.).

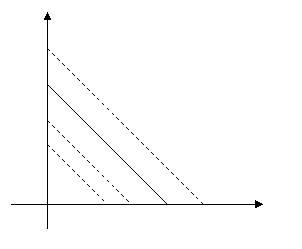
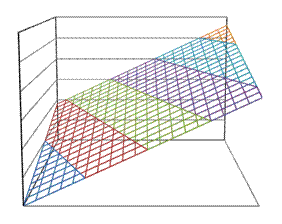
Рис. 1. Линейная производственная функция.

Для функции этого вида легко найти предельные и средние показатели.

,

Эластичность выпуска по каждому из факторов:

, .

Эластичность производства: .

При эластичность производства будет равна 1.

Предельная норма замещения

, .

2. Производственная функция Леонтьева:

.

Эта функция моделирует производственный процесс, в котором факторы производства используются в заданных фиксированных пропорциях, что нередко наблюдается, например, в полностью автоматизированных производственных системах. Любые затраты производственных ресурсов вне заданного соотношения не увеличивают объем производства. Функция учитывает возможность дополнения одних факторов производства другими, но замена одного фактора другим невозможна. Для построения карты изоквант выразим переменную из уравнения

:

, если ,

, если

Таким образом, карту изоквант составляют два семейства линий, параллельных осям координат. Угловые точки изоквант образуют множество оптимальных сочетаний производственных факторов (рис.2.) .

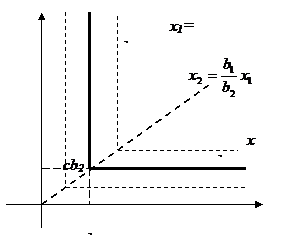
Рис 2. Производственная функция Леонтьева

3. Производственная функция с постоянной эластичностью замены ресурсов CES:

,

где - коэффициент замещения, - коэффициенты распределения, n – степень однородности (нередко полагают ).

Вид изоквант функции CES зависит от значений параметров функции. Например, при изокванты представляют собой выпуклые вниз линии степенного вида, которые имеют горизонтальные и вертикальные асимптоты с уравнениями:

, .

Практически это означает, для таких производственных систем невозможно полностью заменить один ресурс другим. Существуют критические значения затрат факторов, ниже которых производство невозможно.

При других значениях параметров изокванты могут быть прямыми или выпуклыми вверх. Если, то данная функция стремится к производственной функции Кобба-Дугласа, если то получается функция Леонтьева (рис.3.).

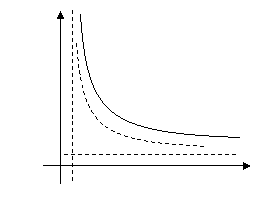
Рис 3. Производственная функция CES.

Производственная функция Кобба-Дугласа

Производственная функция Кобба-Дугласа. занимает особое место в теоретико-экономических исследованиях. В 1929 г. американские исследователи Ч. Кобб и П. Дуглас на основе данных по обрабатывающей промышленности США за период 1899-1922г. представили функцию

,

где K– объем основного капитала, L– затраты труда; b, 𝛼, 𝛽 - положительные параметры. Это была первая эмпирическая производственная функция, построенная по данным временных рядов. Двухфакторная производственная функция степенного вида и сегодня находит широкое применение при изучении закономерностей функционирования экономических систем различных уровней.

Степенная производственная функция вида

, (1)

где называется производственной функцией Кобба-Дугласа. Эта функция задает зависимость объема производства у от двух важнейших производственных факторов – труда (рабочей силы) и основных производственных фондов .

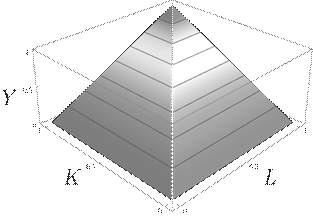
Поскольку функция (1) является функцией двух переменных, ее графиком является поверхность в пространстве переменных , называемая производственной поверхностью. Схематичный рисунок производственной поверхности функции Кобба-Дугласа приведен на рис.4.

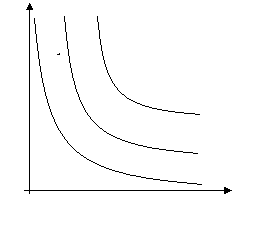
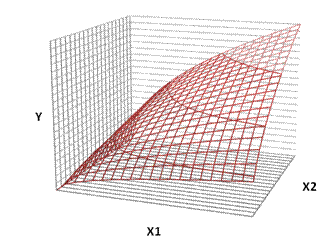
Рис. 1.4 Производственная функция Кобба-Дугласа.

Изокванты производственной функции (1) являются проекциями сечений этой поверхности плоскостями, параллельными плоскости . Они задаются уравнениями вида = С, и могут быть построены как графики функций вида

.

Анализ свойств функции начнем с нахождения предельных и средних величин. Средний по первому ресурсу (труду) продукт есть производительность труда:

Поскольку коэффициент , показатель степени является отрицательной величиной, следовательно, с увеличением затрат труда средняя производительность труда снижается.

Предельной производительностью труда для функции Кобба – Дугласа называют выражение

.

Найдем вторую частную производную функции (1)

Так как , а все остальные множители в правой части положительны, то

Вторая частная производная отрицательна, следовательно, предельная производительность труда с ростом уменьшается. Это свойство отражает хорошо известный в экономической теории закон убывающей предельной эффективности (первый закон Госсена).

Сравнивая предельную и среднюю производительность труда, нетрудно видеть, что

Поскольку , можно сделать вывод, что для производственной функции Кобба-Дугласа предельная производительность труда всегда ниже средней производительности.

Эластичность выпуска по затратам труда вычислим как отношение предельной и средней производительности труда:

Таким образом, параметр выражает процентное увеличение выпуска продукции при увеличении затрат труда на 1%, т. е. характеризует относительный прирост объема производства на единицу относительного увеличения ресурсов труда.

Аналогичные показатели можно рассчитать по отношению ко второму фактору функции Кобба-Дугласа — производственным фондам.

Средний продукт по второму ресурсу – объему основных фондов, называется фондоотдачей:

Фондоотдача выражает объем продукции в расчете на единицу используемых производственных фондов.

Предельная фондоотдача

.

показывает приближенно дополнительный прирост продукции в расчете на дополнительную единицу затраченных производственных фондов. Поскольку , предельная фондоотдача всегда ниже средней.

Эластичность выпуска продукции по объему производственных фондов определяется выражением

Она показывает, на сколько процентов изменится выпуск продукции при увеличении объема фондов на 1%. Как и по отношению к затратам труда, эластичность выпуска по фондам есть величина постоянная, равная коэффициенту регрессии .

Эластичность производства есть сумма эластичностей выпуска по каждому из ресурсов:

Нормы замещения ресурсов для функции Кобба-Дугласа:

, .

Предельная норма замещения первого ресурса вторым:

.

Она показывает, какое количество первого ресурса может быть высвобождено при увеличении затрат второго ресурса на один процент. Аналогично,

Несложно видеть, что предельная норма замещения ресурсов для функции (1.1) зависит не только от параметров функции , но и от соотношения объемов ресурсов.

Параметры , как мы видели выше, являются коэффициентами эластичности функции по соответствующим переменным. Кроме того, они могут использоваться для анализа эффекта расширения производства. Увеличим количество затрачиваемых ресурсов в m раз:

.

Объем производства изменился в раз.

Если эластичность производства , то увеличение ресурсов в m раз приводит к увеличению объема производства также в m раз. Экономически это отвечает предположению, что удвоение числа предприятий какой-либо отрасли приводит к удвоению выпускаемой отраслью продукции.

Если , то увеличение ресурсов опережает увеличение выпуска, т. е. имеем отрицательный эффект расширения производства.

Если , то увеличение выпуска опережает увеличение роста ресурсов. Можно говорить о положительном эффекте расширения.

Линеаризация функции Кобба-Дугласа.

Наряду с уже знакомой нам формой записи функции Кобба-Дугласа (1.1), часто используется другой вид этой функции, более удобный для задач моделирования и прогнозирования, оценивания по экспериментальным данным.

Прологарифмируем уравнение (1) и найдем полный дифференциал функции:

Заменим дифференциалы переменных на приращения этих переменных и получим приближенную формулу:

(2)

Величины и выражают процентные изменения переменных и . Величина соответственно, выражает процентное изменение функции. Тогда полученное соотношение выражает линейную зависимость темпа прироста производства от темпов прироста его факторов.

Производственная функция позволяет исследовать вопросы соотношения, замещения, взаимодействия ресурсов. В частности, в экономике при изучении взаимодействия трудовых ресурсов и производственных фондов определяется такой показатель как фондовооруженность труда. Для функции (1) фондовооруженность труда (капиталовооруженность труда) представляет собой отношение переменных и - норму замены труда капиталом:

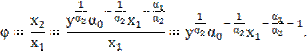
Чем выше фондовооруженность труда, больше единиц живого труда необходимо, чтобы компенсировать единицу снижения объема производственных фондов.

Еще один важный показатель экономического анализа – эластичность замены (замещения) ресурсов. В частности, эластичность замены труда капиталом показывает, на сколько процентов нужно изменить капиталовооруженность труда при изменении предельной нормы замещения труда капиталом на 1% чтобы объем выпуска остался неизменным. Он определяется как отношение относительных приращений фондовооруженности труда и предельной нормы замещения ресурсов:

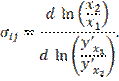
Этот показатель не зависит от единиц измерения, т.к. является величиной относительной. Эластичность замены функции (1) равна 1.

Эластичность замены связана с кривизной изоквант. Она представляет собой тангенс угла наклона изокванты в произвольной точке .

Задачи, решаемые на основе использования производственных функций.

1. Задача обеспечения производства ресурсами.

Производственная функция, в частности, функция Кобба - Дугласа, позволяет рассчитать потребность в одном из ресурсов при заданных объеме производства и величине другого ресурса. Из уравнения (1) несложно выразить объемы ресурсов:

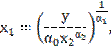
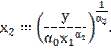
Подставляя в эти соотношения заданные объемы y и , находим искомые значения.

2. Расчет относительных изменений.

Дана производственная функция где y— объем товарной продукции в стоимостном выражении, - фонд заработной платы, - стоимость основных фондов. Произошло изменение величин используемых ресурсов: фонд заработной платы изменился на m %, стоимость основных фондов изменилась на n %. На сколько процентов при этом изменится объем товарной продукции, производительность труда, фондоотдача?

Для решения задачи используем формулу (2):

Величины процентных изменений переменных и соответственно равны m и n. Тогда процентное изменение значения функции равно

Производительность труда является отношением объема товарной продукции к фонду заработной платы . При изменении и новая производительность труда будет равна

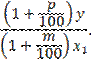
Тогда отношение нового значения производительности труда к старому составит

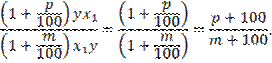
Соответственно, процентное изменение производительности труда равно

Фондоотдача является отношением объема товарной продукции к стоимости основных фондов: . Аналогичные рассуждения позволяют найти величину процентного изменения фондоотдачи:

3. Задачи оптимизации на основе использования производственных функций

Одной из основных задач оптимизации на основе использования производственных функций является задача определения комбинации производственных факторов (ресурсов), обеспечивающей при заданных ограничениях максимальный выпуск продукции. В качестве ограничения в этой задаче часто используют объем переменных издержек при известной стоимости производственных ресурсов. Например, для двухфакторной производственной функции Кобба-Дугласа

, заданных значений цен ресурсов и объема переменных издержек C, задача оптимального выпуска имеет вид:

,

.

Эта задача математического программирования может быть решена методом Лагранжа. Построим функцию Лагранжа.

.

Для нахождения ее стационарных точек приравняем к нулю частные производные.

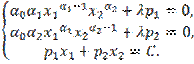
Разделим второе уравнение на первое, предварительно перенеся вторые слагаемые в правую часть, и получим соотношение между компонентами оптимального решения:

Подставив выражение через в последнее равенство системы, получим оптимальное решение:

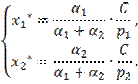
Здесь бюджет переменных издержек С делится между факторами производства пропорционально значениям а затем каждая дробь делится на цену соответствующего ресурса. Подставим найденные значения равновесия производителя в целевую функцию:

.

Прямая, заданная линейным ограничением данной задачи является изокостой. Решение данной задачи в геометрической интерпретации есть точка касания изокосты и наиболее удаленной от начала координат изокванты.

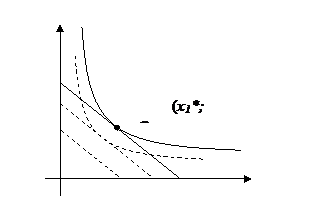
В экономической теории решение приведенной задачи максимизации выпуска называют равновесием производителя. График функции

в пространстве называют оптимальным путем роста.

Для приведенной выше задачи максимизации выпуска можно составить связанную с ней задачу: при заданном уровне выпуска требуется минимизировать переменные издержки. Математическая модель двойственной задачи имеет вид:

,

.

Эта задача также может быть решена методом Лагранжа. Ее оптимальное решение геометрически представляет собой точку касания некоторой линии уровня целевой функции С и нулевой линии уровня функции-ограничения

Нетрудно заметить, что оптимальное решение зависит от объема производства и соотношения цен на ресурсы , задающего наклон линий уровня линейной целевой функции. Значит, оно может быть описано функциями , , которые называют функциями условного спроса на ресурсы. Они позволяют исследовать динамику спроса при изменении заданного уровня производства и цен. Для этого функции условного спроса следует подставить в целевую функцию:

Полученная функция называется функцией расходов. Она определяет минимальные переменные издержки, необходимые для производства единиц продукции при заданных ценах ресурсов и .