Лекция 7. Теория двойственности.

Cоставление двойственных задач

Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования, которую называют двойственной к данной. Исходная и двойственная к ней задача образуют пару двойственных задач.

В зависимости от вида исходной задачи линейного программирования различают симметричные, несимметричные и смешанные пары двойственных задач.

Симметричные пары двойственных задач

Рассмотрим ЗЛП симметричной формы: найти наибольшее значение функции

при ограничениях:

.

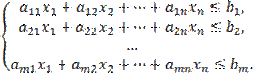
Определение. Если задача линейного программирования представлена в симметричной форме, то вместе с составленной по определенному правилу двойственной задачей они образуют симметричную пару.

Правило составления двойственных задач.

Перед составлением двойственной задачи необходимо согласовать неравенства системы ограничений исходной задачи с целью задачи: если задача на максимум (минимум), то все знаки неравенств в системе ограничений должны быть (≥).

1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная , .

2. Составляется целевая функция , коэффициентами которой будут свободные члены системы ограничений исходной задачи; цель задачи меняется на противоположную:

3. Составляется система ограничений двойственной задачи. Матрица коэффициентов системы ограничений исходной задачи транспонируется, знаки неравенств меняются на противоположные. Свободными членами неравенств являются коэффициенты целевой функции исходной задачи:

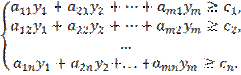
4. Переменные в двойственной задаче также неотрицательны, т.е.

Получена двойственная задача: найти наименьшее значение функции

при ограничениях:

.

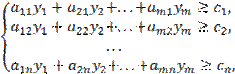
Если полученную задачу принять за исходную и по указанному выше правилу составить двойственную к ней, то получим исходную задачу вида.

Несимметричные и смешанные пары двойственных задач

Определение. Если ЗЛП задана в каноническом виде:

,

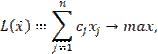
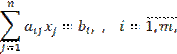
то вместе с двойственной к ней задачей они образуют несимметричную пару.

Определение. Если ЗЛП задана в общем виде:

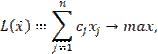
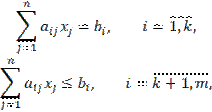
то вместе с двойственной к ней задачей они образуют смешанную пару.

В несимметричной и смешанной парах целевая функция и матрица системы ограничений двойственной задачи составляется по тем же правилам, что и в случае симметричной пары, а остальные этапы построения отличны.

Правило составления двойственных задач.

1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная , .

2. Составляется целевая функция , коэффициентами которой будут свободные члены системы ограничений исходной задачи; цель задачи меняется на противоположную:

.

3. Составляется система ограничений двойственной задачи. Матрица коэффициентов системы ограничений исходной задачи транспонируется.

4. Если двойственная переменная поставлена в соответствие ограничению в форме уравнения, то эта переменная свободна по знаку: . Если двойственная переменная соответствует неравенству, то она неотрицательна. И обратно, если переменная исходной задачи неотрицательна то соответствующее ей ограничение двойственной задачи является неравенством со знаком ³. (Если составляется задача на максимум, то знак неравенства будет ). Если переменная исходной задачи произвольна по знаку, то в двойственной задаче ей соответствует уравнение.

Пример. Составить двойственную задачу для ЗЛП:

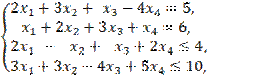
х₁ ³ 0, х₂ ³ 0.

Решение. Все неравенства системы ограничений согласованы с целью задачи. Поставим в соответствие каждому ограничению двойственную переменную:

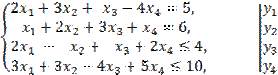
Составим целевую функцию как сумму произведений свободных членов системы ограничений исходной задачи на двойственные переменные. Цель задачи изменим на противоположную:

Составим матрицу системы ограничений. Для этого матрицу коэффициентов системы ограничений исходной задачи транспонируем:

→

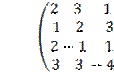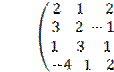
Поскольку переменные х₁ ³ 0, х₂ ³ 0, то соответствующие им первое и второе ограничения двойственной задачи будут неравенствами со знаком . Остальные переменные х₃, х₄, х₅ произвольны по знаку, значит, третье, четвертое и пятое ограничения будут уравнениями.

Третье и четвертое ограничения исходной задачи представлены неравенствами, следовательно переменные у₃ и у₄ должны быть неотрицательны.

Двойственная задача вид:

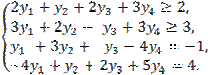
Основные теоремы теории двойственности

Пусть дана симметричная пара двойственных задач (3.14), (3.18).

Теорема. (первая основная теорема двойственности). Если одна из двойственных задач имеет оптимальное решение, то и другая задача также имеет оптимальное решение, причем экстремальные значения целевых функций равны:

.

Если одна из двойственных задач не имеет оптимального решения из-за неограниченности целевой функции, то другая задача также не имеет оптимального решения, причем из-за несовместности системы ограничений.

Теорема. (вторая основная теорема двойственности). Для того чтобы допустимые решения и несимметричной пары двойственных задач были соответственно оптимальными решениями, необходимо и достаточно, чтобы выполнялись равенства:

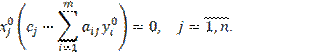
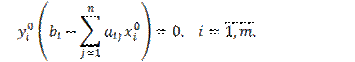
Следствие. Если в оптимальном решении одной из двойственных задач какая-либо переменная не равна нулю, то соответствующее ей ограничение двойственной задачи на оптимальном решении выполняется как равенство. И наоборот: если на оптимальном решении одной из двойственных задач какое-либо ограничение выполняется как строгое неравенство, то соответствующая ему переменная в оптимальном решении двойственной задачи равна нулю.

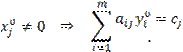
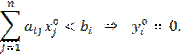
Экономическая интерпретация двойственных задач

Пусть дана ЗЛП об оптимальном использовании ресурсов: необходимо найти план производства, обеспечивающий максимальную прибыль при ограниченных запасах ресурсов, известных нормах затрат ресурсов и прибыли на единицу продукции. Математическая модель задачи: найти наибольшее значение функции

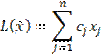
при ограничениях:

.

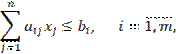
Предположим, что есть решение о продаже имеющихся ресурсов (без производства продукции). Необходимо определить минимальные цены на ресурсы, такие, чтобы прибыль от продажи сырья была не меньше, чем прибыль от продажи изготовленной из этого сырья продукции.

Составим математическую модель задачи. Пусть - цены предлагаемых к продаже ресурсов. Целевая функция выражает суммарную прибыль от продажи и является суммой произведений запасов ресурсов на цены ресурсов:

Для составления системы ограничений учтем, что общая стоимость сырья в единице продукции должна быть не меньше цены изделия:

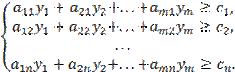
Цены ресурсов неотрицательны:

Получена двойственная задача:

.

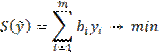
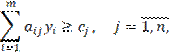
В соответствии с таким подходом, величины называют двойственными ценами.

Свойства двойственных решений.

1. Установим размерность двойственных переменных . Из ограничений двойственной задачи

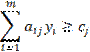
следует, что размерность произведения совпадает с размерностью т.е. ( знак означает эквивалентность размерности). Тогда:

Таким образом, измеряется в рублях на единицу ресурса.

2. Если при оптимальном плане производства (на оптимальном решении) какое-либо ограничение задачи выполняется как строгое неравенство

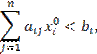
то это означает, что расход данного ресурса строго меньше его запаса. Такой ресурс имеется в избытке и не расходуется полностью при оптимальном плане. Тогда, согласно второй теореме двойственности, i- я координата оптимального решения равена нулю .

Если же i- й ресурс имеет ненулевую двойственную цену , то согласно теореме верно равенство:

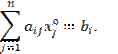
Тогда запас этого ресурса полностью расходуется при оптимальном плане производства, т.е. данный ресурс является дефицитным.

Эти рассуждения позволяют сделать вывод о том, что оптимальные решения двойственной задачи можно расценивать как меру дефицитности ресурса. Поэтому компоненты оптимального решения называют также двойственными оценками ресурсов. Чем больше значение двойственной оценки , тем более дефицитным является ресурс. Недефицитный ресурс имеет нулевую оценку.

3. Двойственные оценки можно рассматривать также как меру влияния свободных членов системы ограничений исходной задачи на значение целевой функции. Согласно теореме (3.6),

,

.

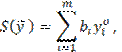
Прирост оптимальной прибыли пропорционален приращению i-го ресурса, причем коэффициент пропорциональности равен . Другими словами, величина двойственной оценки показывает, на сколько единиц возрастет значение целевой функции при увеличении запаса соответствующего ресурса на единицу. Заметим, что этот вывод справедлив лишь для малых приращений ресурса (в пределах устойчивости решения). При значительных изменениях запаса ресурса может измениться само оптимальное решение.

Нахождение оптимального решения двойственной задачи

Основные теоремы двойственности позволяют по решению одной из двойственных задач найти оптимальное решение другой.

Нахождение решения двойственной задачи в несимметричной паре

Пример. Найти решения двойственных задач, одна из которых имеет вид:

х_j ³ 0, .

Решение. Данная ЗЛП решена методом искусственного базиса, получено оптимальное решение Назовем ее X - задачей. Составим двойственную Y - задачу: найти наименьшее значение функции

при ограничениях:

.

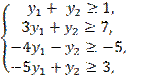
Согласно первой теореме двойственности, оптимальное решение Y-задачи существует и оптимальные значения целевых функций равны:

Воспользуемся следствием из второй теоремы двойственности. Т.к. в оптимальном решении X-задачи и , то на оптимальном решении Y- задачи соответствующие ограничения (второе и третье) выполняются как уравнения:

Решая эту систему, получим у₁ = –2, у₂ = 13.

Ответ:

Нахождение решения двойственной задачи в симметричной паре

Пример. Для ЗЛП, найти решения двойственной задачи, используя теоремы двойственности.

Решение. Запишем исходную ЗЛП:

,

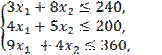
х₁ ³ 0 , х₂ ³ 0.

Назовем ее X – задачей. Эта задача решена графически, получено оптимальное решение:

, , .

Составим двойственную задачу:

min

у_i ³ 0, .

Назовем ее Y- задачей. Из первой теоремы двойственности следует, что оптимальное решение Y- задачи существует, а оптимальные значения целевых функций равны:

.

Для нахождения решения Y- задачи применим вторую теорему двойственности (точнее, ее следствие). Т.к. в оптимальном решении X-задачи и , то при оптимальном решении Y- задачи соответствующие ограничения (первое и второе) выполняются как равенства:

Получена неопределенная система линейных уравнений. Для того чтобы доопределить систему, снова воспользуемся следствием из второй теоремы двойственности. Подставим оптимальное решение X-задачи в условия X-задачи и получим, что третье ограничение выполняется как строгое неравенство:

Тогда согласно теореме о равновесии (следствию из второй основной теоремы двойственности), соответствующая переменная в оптимальном решении Y- задачи равна нулю:

у₃ = 0.

Получена система трех уравнений с тремя неизвестными:

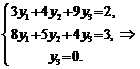
Решая систему, получим .

Второй способ нахождения решения двойственной задачи в симметричной паре

Если двойственные задачи образуют симметричную пару, то одну из них можно решить симплексным методом, а решение второй найти по оценочной строке симплексной таблицы. Для этого нужно установить соответствие между основными переменными одной задачи и балансовыми переменными другой.

Запишем системы ограничений симметричной пары двойственных задач.

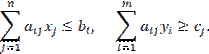
Приведем их к каноническому виду. Для X-задачи:

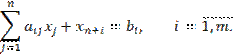
Здесь переменные – основные, а переменные – балансовые.

Аналогично для Y – задачи:

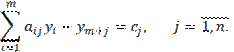
Переменные – основные, а – балансовые.

В симметричной паре двойственных задач основные переменные оптимального решения одной задачи равны модулям оценок балансовых переменных оптимального решения другой задачи:

.

.

Пример. Найти решения двойственных задач, одна из которых имеет вид:

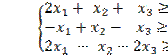
х_j ³ 0, .

Решение. Составим двойственную задачу:

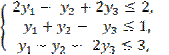
у_i ³ 0,

Решим Y-задачу симплексным методом. Для этого приведем ее к каноническому виду.

.

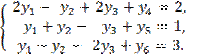
Приведем решение в виде симплексной таблицы:

сj	Б.п.	5	8	4	0	0	0
		у1	у2	у3	у4	у5	у6	bi
0 0 0	у4 у5 у6	2 1 1	–1 1 –1	2 –1 –2	1 0 0	0 1 0	0 0 1	2 1 3
		–5	–8	–4	0	0	0	0
0 8 0	у4 у2 у6	3 1 2	0 1 0	1 –1 –3	1 0 0	1 1 1	0 0 1	3 1 4
		3	0	–12	0	8	0	8
4 8 0	у3 у2 у6	3 4 11	0 1 0	1 0 0	1 1 3	1 2 4	0 0 1	3 4 13
		39	0	0	12	20	0	44

Получено оптимальное решение Y-задачи: , .

По первой теореме двойственности оптимальное решение X – задачи существует и . Установим связь между переменными: основным переменным соответствуют балансовые переменные . Значения переменных в оптимальном решении равны модулям оценок , выпишем их из последней строки симплексной таблицы:

.

Ответ: , .