Лекция 6. Симплексный метод решения ЗЛП.

Симплексный метод является универсальным методом решения ЗЛП канонического вида с произвольным количеством переменных. Он относится к группе методов последовательного приближения. Согласно теоремам, если оптимальное решение ЗЛП существует, то оно совпадает хотя бы с одним из опорных решений. Симплексный метод позволяет выполнить упорядоченный перебор опорных решений. В каждой новой итерации находится опорное решение, при котором значение целевой функции будет ближе к оптимальному.

Теоретические основы симплексного метода.

Пусть дана ЗЛП в канонической форме:

,

Предположим, что система ограничений имеет ранг r<n и ее можно разрешить относительно некоторого неотрицательного базиса, содержащего r переменных x₁, x₂, …,x_r. Это можно сделать, например, используя метод Жордана – Гаусса. Преобразование системы линейных уравнений в этом случае предполагает последовательное исключение неизвестных x₁, x₂, …,x_r. Решение как правило выполняют в табличной форме.

Базис						bi
	х1	…	xj	…
	…	… …. …	…	… … …	…	…

В исходную таблицу записывают расширенную матрицу системы. Далее приступают к выполнению очередной итерации:

1. Выбирают ключевой элемент преобразования:

а) в качестве ключевого столбца выбирают любой столбец коэффициентов при неизвестных, если в нем есть хотя бы один положительный элемент;

б) в качестве ключевой строки берется та, у которой отношение свободного члена к положительному элементу ключевого столбца минимально.

На пересечении ключевой строки и ключевого столбца находится ключевой элемент.

2. Элементы ключевой строки делят на ключевой элемент.

3. Ключевой столбец заполняют нулями.

4. Остальные элементы вычисляют по правилу прямоугольника: составляют прямоугольник, в противоположных вершинах которого находятся ключевой элемент и пересчитываемый элемент; из произведения элементов, стоящих на диагонали прямоугольника с ключевым элементом, вычитают произведение элементов другой диагонали и полученную разность делят на ключевой элемент.

В результате соответствующая переменная исключается из системы и становится базисной. Аналогично исключаются другие базисные переменные. Количество исключенных переменных равно рангу системы уравнений r. Система ограничений задачи принимает вид:

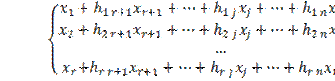
Получено опорное решение .Найдем значение целевой функции на этом опорном решении:

= .

Коэффициенты

,

называются оценками свободных переменных

Критерий оптимальности опорного решения для ЗЛП на максимум:

1) Если все оценки , то найденное опорное решение оптимально.

2) Если среди оценок имеется хотя бы одна отрицательная , то найденное опорное решение не оптимально. Тогда если среди коэффициентов при есть хотя бы одно положительное число, то переменную можно ввести в базис и получить большее значение целевой функции .

Если и все коэффициенты при неположительные ( £ 0), то в базис ввести нельзя. Покажем, что в этом случае . Для этого из системы выпишем общее решение, и всем свободным переменным, кроме , придадим значение, равное 0:

.

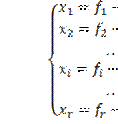
Отсюда видно, что если придавать сколь угодно большие числовые значения, то решение, полученное из системы будет допустимым, а значение целевой функции будет неограниченно расти. Решение задачи на максимум не существует.

3) Предположим, что найдено оптимальное решение задачи, все оценки , и хотя бы одна из оценок свободных переменных равна нулю. Это говорит о наличии в задаче альтернативного оптимума. Если ввести в базис свободную переменную с нулевой оценкой, то получим второе оптимальное решение, а значение целевой функции при этом не изменится. Кроме того, на основании теоремы любая выпуклая линейная комбинация двух оптимальных решений также будет оптимальным решением с тем же значением целевой функции.

Если нулевых оценок свободных переменных окажется несколько, то введение в базис каждой из этих переменных приводит к получению различных опорных оптимальных решений. Тогда задача имеет множество оптимальных решений, каждое из которых является выпуклой линейной комбинацией опорных оптимальных решений.

Алгоритм симплексного метода

Решение ЗЛП симплексным методом предполагает выполнение следующих этапов:

1. Привести задачу к каноническому виду.

2. Записать систему ограничений в форме симплекс-таблицы с неотрицательными свободными членами.

Ci	Базис		…		…		bi
		х1	…	xj	…
		…	… …. …	…	… … …	…	…

3. Найти неотрицательное базисное решение системы ограничений (первоначальное опорное решение).

4. Проверить найденное опорное решение на оптимальность. Для этого найти оценки свободных переменных по формуле

, ,

где - коэффициент целевой функции при переменной ,

– коэффициент целевой функции при базисной переменной – го уравнения ( – й строки симплексной таблицы),

– коэффициент – го уравнения ( – й строки симплексной таблицы) при переменной .

Если все оценки , то найденное решение оптимально, задача решена.

Если хотя бы одна оценка D_j < 0, а при соответствующей переменной х_j нет ни одного положительного коэффициента, то задача не имеет оптимального решения из-за неограниченности целевой функции.

Если хотя бы одна оценка D_j < 0, а при соответствующей переменной есть хотя бы один положительный коэффициент, то найденное решение не оптимально. Следует выполнить переход к другому опорному решению, введя в базис переменную с отрицательной оценкой, и снова проверить решение на оптимальность. Если отрицательных оценок несколько, то в базис вводят переменную с наибольшей по абсолютной величине отрицательной оценкой.

Замечание 1. Критерием оптимальности для ЗЛП на минимум является условие

Замечание 2. Если среди неотрицательных оценок свободных переменных оптимального решения присутствует хотя бы одна нулевая , то задача имеет альтернативный оптимум. Для его нахождения нужно ввести в базис свободную переменную с нулевой оценкой. Ответ следует записать в виде выпуклой линейной комбинации оптимальных решений.

Пример. Найти наибольшее значение функции

при ограничениях:

.

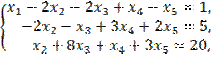
Решение. Задача имеет канонический вид. Найдем первоначальное опорное решение. Запишем данные в таблицу.

Базис	х1	х2	х3	х4	х5	bi
x1	1 0 0	–2 –2 1	–2 –1 8	1 3 1	–1 2 3	1 5 20

Переменная является исключенной, поскольку содержится только в первом уравнении с коэффициентом 1. Значит, ее можно считать вошедшей в базис и отметить этот факт записью в левом столбце. Выберем новый ключевой элемент. Пусть, например, это будет положительный коэффициент . Создадим единичный столбец при переменной перейдем к следующей таблице, используя правило прямоугольника:

Базис	х1	х2	х3	х4	х5	bi
x1 x2	1 0 0	0 0 1	14 15 8	3 5 1	5 8 3	41 45 20

Переменная введена в базис. Следующий ключевой элемент выберем из второй строки, поскольку в ней еще нет исключенной переменной. Пусть это будет коэффициент , он отвечает требованиям выбора ключевого элемента:

Базис	х1	х2	х3	х4	х5	bi
x1 x5 x2	1 0 0	0 0 1	37/8 15/8 19/8	–1/8 5/8 –7/8	0 1 0	103/8 45/8 25/8

Получено опорное решение. Выпишем его, используя значения правого столбца для базисных переменных , а свободные переменные примем равными 0:

.

Проверим это решение на оптимальность. Рассчитаем оценки . Для этого добавим в таблицу слева столбец C_i и впишем в него коэффициенты целевой функции при базисных переменных . Коэффициенты этого столбца будем поочередно умножать на элементы столбца с номером j, для которого рассчитывается оценка , суммировать, а затем из полученной суммы вычтем коэффициент целевой функции, надписанный в верхней строке j – го столбца.

Ci	Базис	1	1	– 5	2	1	bi
		х1	х2	х3	х4	х5
1 1 1	x1 x5 x2	1 0 0	0 0 1	37/8 15/8 19/8	–1/8 5/8 –7/8	0 1 0	103/8 45/8 25/8
D j		0	0	111/8	–19/8	0	173/8

Найденное решение не оптимально, так как D₄<0. Введем в базис свободную переменную с отрицательной оценкой х₄. Для этого выберем в четвертом столбце ключевой элемент. Единственно возможный вариант выбора – неотрицательный коэффициент 5/8. Выполним пересчет таблицы вместе со строкой оценок используя преобразование Жордана.

Ci	Базис	1	1	–5	2	1	bi
		х1	х2	х3	х4	х5
1 2 1	x1 x4 x2	1 0 0	0 0 1	5 3 5	0 1 0	1/5 8/5 7/5	14 9 11
D j		0	0	21	0	19/5	43

Получено второе опорное решение .

Так как среди оценок нет отрицательных чисел, то это опорное решение оптимально.

Ответ: , .