Лекция 5. ЗЛП. Математические модели экономических задач. Графический метод решения ЗЛП

1. Задачи линейного программирования, классификация и свойства

Определение 1. Задача, в которой требуется найти экстремум функции

при ограничениях:

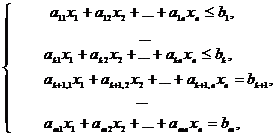
называется общей задачей линейного программирования (ЗЛП).

Задача в краткой форме записи имеет вид:

, .

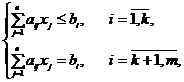
Определение 2. Задача, в которой требуется найти экстремум функции

при ограничениях:

,

называется задачей линейного программирования, представленной в канонической форме (система ограничений задана уравнениями).

Определение 3. Задача, в которой требуется найти экстремум функции

при ограничениях:

,

называется задачей линейного программирования, представленной в симметричной (неканонической) форме записи (система ограничений задана неравенствами).

Определение 4. Функция, наибольшее или наименьшее значение которой нужно найти при данных ограничениях задачи

называется целевой функцией ЗЛП.

Определение 5. Совокупность чисел удовлетворяющая ограничениям ЗЛП, называется допустимым решением ЗЛП.

Определение 6. Допустимое решение, при котором целевая функция принимает максимальное (минимальное) значение, называется оптимальным решением ЗЛП.

2. Переход от одной формы ЗЛП к другой

Переход от симметричной формы ЗЛП к канонической.

Теорема 1. Каждому решению неравенства

соответствует единственное решение уравнения

и неравенства , и наоборот.

Из теоремы следует, что неравенство

можно заменить уравнением

и неравенством

.

Переменную называют балансовой переменной.

Чтобы привести задачу к каноническому виду, нужно заменить каждое неравенство системы ограничений соответствующим уравнением, введя в каждое неравенство неотрицательную балансовую переменную с коэффициентом + 1, если знак неравенства £, и с коэффициентом – 1, если знак неравенства ³. В целевую функцию балансовые переменные вводятся с нулевыми коэффициентами. Неотрицательность балансовых переменных также отражается в системе ограничений.

Переход от канонической формы ЗЛП к симметричной форме.

Чтобы перейти от канонической формы ЗЛП к симметричной, нужно найти общее решение системы уравнений:

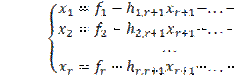
Так как все переменные (в том числе и базисные) неотрицательны, отбросив базисные переменные получим систему неравенств:

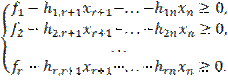
Эта система неравенств является системой ограничений задачи в симметричной форме. Затем необходимо исключить базисные переменные из целевой функции. Для этого в целевую функцию нужно вместо базисных переменных подставить их выражения через свободные переменные.

Пример1. Привести к каноническому виду следующую задачу линейного программирования:

→max

.

Введем в первое неравенство балансовую переменную с коэффициентом 1 и преобразуем неравенство в уравнение. Введем во второе неравенство балансовую переменную с коэффициентом -1. Аналогично преобразуем третье неравенство.

Получили ЗЛП в каноническом виде: найти наибольшее значение функции

при ограничениях:

.

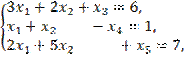
Пример 2. Привести к симметричному виду задачу линейного программирования:

.

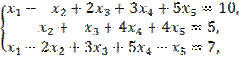
Разрешим систему относительно базиса Получим общее решение:

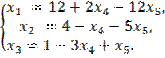
Отбрасывая в каждом уравнении системы базисные переменные , , получим систему неравенств

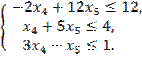
Выразим целевую функцию через свободные переменные:

Получили ЗЛП в симметричном виде: найти наибольшее значение функции

при ограничениях:

.

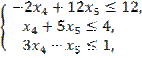
3. Математические модели экономических задач

Задача об оптимальном использовании ресурсов (о планировании производства)

Предприятие выпускает несколько видов продукции, используя для этого различные ресурсы. Известны затраты каждого вида ресурса на производство единицы каждого вида продукции и прибыль от реализации единицы каждого вида продукции. Требуется составить план выпуска продукции, чтобы при данных запасах ресурсов получить максимальную прибыль.

Составим математическую модель задачи.

Введем обозначения:

i — номер ресурса, ;

b_i — запас ресурса i-го вида, ;

j — номер продукции, ;

a_ij — затраты i-го вида ресурса на производство единицы j-го вида продукции;

c_j — прибыль от реализации единицы j-го вида продукции.

Все данные занесем в табл. 1:

Таблица 1

Виды Виды продукции ресурсов	1 2 … j … n	Запасы ресурсов
1 2 … i … m	a11 a12 … a1j … a1n a21 a22 … a2j … a2n … ai1 ai2 … aij … ain … am1 am2 … amj … amn	b1 b2 … bi … bm
Прибыль от реализации единицы продукции	c1 c2 … cj … cn

Обозначим через x_j — планируемый выпуск j-го вида продукции, x_j ≥ 0. Тогда — план выпуска продукции. Составим целевую функцию, выражающую суммарную прибыль от реализации всей выпускаемой продукции:

c₁x₁ + c₂x₂ + … + c_jx_j + … + c_nx_n.

Необходимо найти наибольшее значение этой функции при наличии условий, связанных с ограниченностью запасов сырья (ресурсов).

Составим ограничения по запасам ресурсов. Расход первого ресурса на производство всей продукции не должен превышать имеющегося объема b₁:

a₁₁x₁ + a₁₂x₂ + … + a_1j х_j + … + a_1n x_n £ b₁.

Аналогично составляем ограничения по другим видам ресурсов.

Исходная задача сводится к следующей задаче: найти наибольшее значение функции

при ограничениях:

.

Таким образом, математической моделью задачи об оптимальном использовании ресурсов является ЗЛП.

Пример Для производства двух видов продукции используется три вида сырья. Расход сырья на производство единицы продукции, запасы сырья, а также прибыль от реализации единицы продукции каждого вида заданы в таблице.

Виды Виды сырья продукции	1 2	Запасы сырья, кг
1 2 3	3 8 4 5 9 4	240 200 360
Прибыль от реализации единицы продукции, у.е.	2 3

Составить план выпуска продукции, обеспечивающий максимальную прибыль.

Составим математическую модель задачи. Обозначим через х₁, х₂) план выпуска продукции. Составим функцию прибыли. При реализации ед. первой продукции будет получено у.е. прибыли, при реализации ед. второй продукции будет получено у.е. прибыли. Целевая функция задачи имеет вид:

.

Составим ограничение по первому виду сырья. Согласно условию, 3х₁ + 8х₂ — расход первого вида сырья на выпуск х₁ ед. первого вида продукции и х₂ ед. второго вида продукции. Эта сумма не должна превышать запасов сырья: 3х₁ + 8х₂ £ 240. Аналогично составляем ограничения по второму и третьему видам сырья. Очевидно, х₁ ³0, х₂ ³0.

Таким образом, математическая модель задачи:

→ max

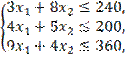
х₁ ³0, х₂ ³0.

Получена задача линейного программирования.

4. Геометрическая интерпретация ЗЛП

Рассмотрим линейное неравенство с двумя неизвестными

.

Его решением на плоскости Х₁ОХ₂ является полуплоскость, ограниченная прямой

Решением системы m линейных неравенств с двумя неизвестными

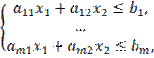
является пересечение полуплоскостей, ограниченных прямыми

, .

Это пересечение полуплоскостей как правило представляет собой выпуклый многоугольник с конечным числом угловых точек (рис. 1).

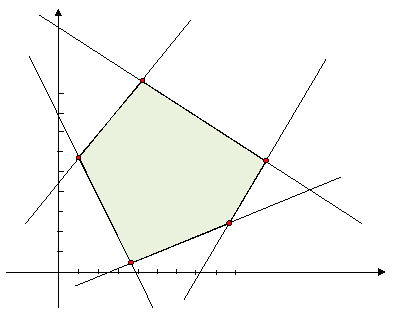
Рис. 1.

В отдельных случаях область решений системы линейных неравенств с двумя переменными может являться выпуклой неограниченной областью с одной или несколькими угловыми точками; единственной точкой; пустым множеством.

Рассмотрим задачу линейного программирования неканонического вида с двумя переменными. Напомним, что в системе ограничений такой задачи содержится m линейных неравенств с двумя неизвестными, а переменные задачи неотрицательны. В соответствии со сказанным выше, областью решений системы ограничений задачи является выпуклая область, ограниченная прямыми (многоугольник). Каждая точка этой области является решением системы линейных неравенств, ее координаты удовлетворяют всем неравенствам системы. Неотрицательный сегмент многоугольника является областью допустимых решений (ОДР) задачи. Для решения задачи необходимо среди всех точек многоугольника ОДР выбрать такую (такие), в которой целевая функция принимает наибольшее значение.

Выпуклые многоугольники обладают рядом характерных свойств, которые будут использованы в дальнейшем изложении. В частности, любая граничная точка выпуклого многоугольника может быть представлена в виде выпуклой линейной комбинации пары угловых точек:, , .

Любая внутренняя точка выпуклого многоугольника может быть представлена в виде выпуклой линейной комбинации его угловых точек:

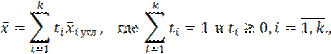
Теперь перейдем к рассмотрению случая n переменных. Неравенство вида

по аналогии с приведенным выше двухмерным случаем, задает в пространстве полупространство, ограниченное гиперполуплоскостью

В случае произвольного количества переменных система m линейных неравенств с n неизвестными имеет вид:

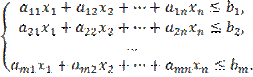
Решение такой системы - многомерный аналог выпуклого многоугольника, его называют выпуклым пространственным многогранником с конечным числом угловых n- мерных точек. Он представляет собой область пересечения полупространств, каждое из которых есть решение одного из неравенств системы.

Таким образом, для решения симметричной ЗЛП с произвольным количеством неизвестных необходимо среди всех точек многогранника области допустимых решений системы ограничений выбрать такую (такие), в которых целевая функция принимает наибольшее значение.

Для ЗЛП канонического вида область допустимых решений также представляет собой ограниченное или неограниченное выпуклое множество, являющееся пересечением гиперплоскостей - множеств, заданных уравнениями вида

.

Вершинами (угловыми точками) такого многогранника решений являются опорные решения системы ограничений – неотрицательные базисные решения. Каждой вершине многогранника ОДР соответствует опорное решение системы ограничений, и наоборот. Если ранг системы ограничений , то многогранник ОДР имеет конечное число вершин, не превышающее .

5. Теоремы об экстремуме целевой функции

Теорема 2. Если область допустимых решений (ОДР) системы ограничений ЗЛП непуста и ограничена, то оптимальное решение ЗЛП существует и совпадает хотя бы с одним из опорных решений системы ограничений.

Теорема 3. Если область допустимых решений ЗЛП не ограничена, то оптимальное решение существует и совпадает хотя бы с одним из опорных решений, если целевая функция ограничена сверху на ОДР в задаче на максимум (снизу - в задаче на минимум).

Определение 7. Ситуация, когда оптимальное решение ЗЛП совпадает с несколькими опорными решениями, называется случаем альтернативного оптимума.

Теорема 4. Если оптимальное решение ЗЛП совпадает с несколькими опорными решениями, то любая выпуклая линейная комбинация этих оптимальных решений также является оптимальным решением задачи.

Следствие. Если ЗЛП имеет два оптимальных решения и , то любая точка отрезка также является оптимальным решением. Другими словами, множество точек оптимальности можно записать в виде:

, где 0 £ t £ 1.

Из теорем 3.2 - 3.4 следует, что оптимальное решение ЗЛП следует искать только среди опорных решений системы ограничений. Так как опорные решения соответствуют угловым точкам ОДР, то оптимальные решения следует искать среди угловых точек ОДР.

6 Графический метод решения ЗЛП

Графическим методом можно решать задачи линейного программирования с двумя переменными, представленные в неканоническом виде, или сводящиеся к ним. Рассмотрим следующую задачу: найти экстремум функции

при ограничениях:

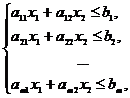
х₁³0, х₂³0.

На первом этапе строится область допустимых решений. Для этого на плоскости Х₁ОХ₂ нужно построить полуплоскости, являющиеся решениями неравенств, а затем найти часть их пересечения, попавшую в первый квадрант.

Возможны следующие ситуации.

1) Область допустимых решений — пустое множество. Тогда ЗЛП не имеет оптимального решения из-за несовместности системы ограничений.

2) Область допустимых решений — единственная точка. Это единственное решение и будет оптимальным решением.

3) Область допустимых решений — выпуклый многоугольник. В этом случае, согласно теоремам 3.2 – 3.4., оптимальное решение следует искать среди угловых точек ОДР. Для этого можно найти координаты всех угловых точек многоугольника, вычислить значения целевой функции в этих точках и выбрать наибольшее (наименьшее). Координаты соответствующей угловой точки будут оптимальным решением.

Существует и другой способ выбора оптимальной точки, основанный на использовании градиента. Вектор — градиент целевой функции

показывает направление, в котором целевая функция возрастает с наибольшей скоростью. Соответственно, чем более продвинута в этом направлении угловая точка ОДР, тем большее значение принимает целевая функция в этой точке. Значит, в качестве оптимального решения нужно выбрать угловую точку ОДР, наиболее удаленную в направлении градиента.

Для практической реализации этой задачи можно построить одну из линий уровня целевой функции - прямую, перпендикулярную градиенту. Смещение линии уровня в направлении градиента до момента выхода из ОДР укажет нужную угловую точку.

Замечание 1. При решении задачи на нахождение наименьшего значения целевой функции (задачи на минимум) линию уровня смещают в направлении антиградиента.

Замечание 2. Если экстремум достигается одновременно в двух угловых точках, то по теореме об альтернативном оптимуме оптимальным решением будет любая точка отрезка, соединяющего эти точки:

, .

4) Область допустимых решений — выпуклая неограниченная область. В данном случае оптимальное решение может совпадать с одной угловой точкой, с частью границы ОДР (альтернативный оптимум), а может и не существовать в силу неограниченности целевой функции сверху на ОДР (или снизу - в задаче на минимум).

Пример Решить графически задачу.

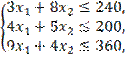
х₁ ³0, х₂ ³0.

Решение. Построим область допустимых решений на плоскости Х₁ОХ₂.

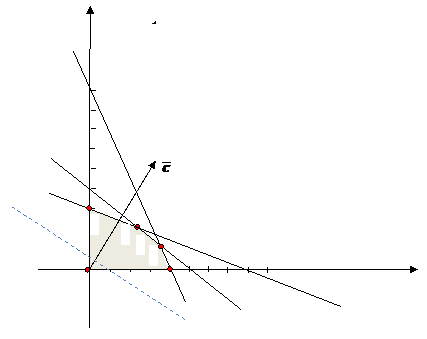
Рис. 2.

Областью допустимых решений является выпуклый пятиугольник ОАВCD (рис. 2).

Построим вектор , коллинеарный вектору и линию уровня, перпендикулярную вектору (пунктирная линия на рис. 3.2). Будем смещать линию уровня в направлении градиента. Наибольшее значение целевая функция достигает в наиболее удаленной угловой точке В. Определим точку В как точку пересечения прямых (1) и (2). Решим систему соответствующих уравнений:

Получим: , . Тогда .

Ответ: , .

Пример Найти наибольшее и наименьшее значения функции

при ограничениях:

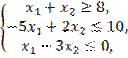
х₁ ³0, х₂ ³0.

Решение. Задача с двумя переменными в симметричной форме. Для решения применим графический метод. Построим ОДР.

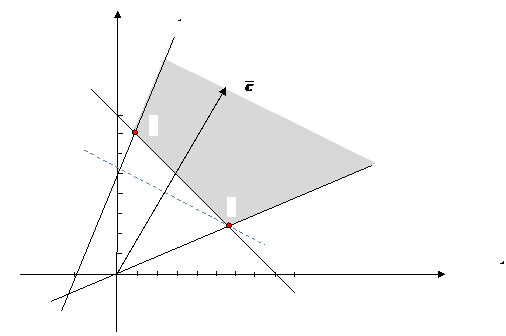
Рис. 3.

Областью допустимых решений системы ограничений является выпуклая неограниченная область с угловыми точками A и B (рис. 3). Наименьшее значение целевой функции достигается в угловой точке B, поскольку именно через эту точку проходит линия уровня, наиболее удаленная в направлении антиградиента (пунктирная линия на рис. 3.3). Найдем координаты точки B как точки пересечения прямых (1) и (3). для этого решим систему соответствующих уравнений:

Из чертежа видно, что невозможно определить угловую точку ОДР, наиболее удаленную в направлении градиента., Целевая функция не ограничена сверху на ОДР, и следовательно она не имеет наибольшего значения на ОДР.

Ответ: .