Лекция 4. Условная оптимизация
Экстремумы
функций многих переменных
Рассмотрим функцию n переменных
.
Определение 13. Точка 
называется
точкой локального максимума (минимума) функции, если найдется некоторая
окрестность данной точки, для всех точек которой выполняется условие 
.
Определение 14. Точки локального максимума и минимума
называются точками экстремума.
Теорема 6 (необходимое
условие экстремума функции). Если точка является точкой
локального экстремума функции, то в этой точке все частные производные равны
нулю.
Определение 12.15. Точки, в которых частные производные
равны нулю называются стационарными точками функции многих переменных.
Стационарные точки являются
точками, "подозрительными" на экстремум.
Необходимое условие экстремума не является достаточным, т.е. не каждая стационарная
точка является точкой экстремума.
Например, функция 
имеет частные
производные
, 
.
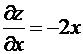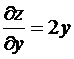В точке (0,0) частные производные функции равны нулю, однако в этой точке
у функции нет экстремума. Данная точка является седловой точкой графика (рис.
12.8).
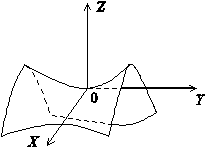
Рис. 12.8
Определение 16. Матрица, составленная из значений
частных производных второго порядка, вычисленных в некоторой точке называется матрицей
Гессе
,
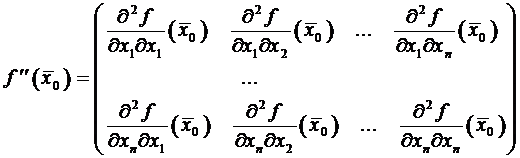или в сокращенном виде
.
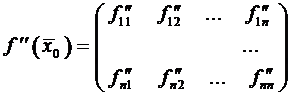Определение 17. Матрица Гессе называется положительно (отрицательно)
определенной, если для любого вектора приращения 
справедливо
соотношение 
.
Теорема 7 (критерий
Сильвестра). Необходимым и
достаточным условием положительной определенности матрицы Гессе 
является
выполнение n условий:
,
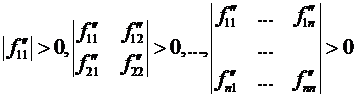т.е.
необходимо и достаточно, чтобы все левые верхние миноры этой матрицы были положительны.
Необходимым и достаточным условием отрицательной определенности матрицы
является выполнение следующих условий:
,
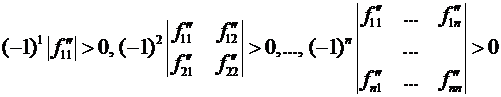т.е.
необходимо и достаточно, чтобы левые верхние миноры нечетных порядков были отрицательны, а
миноры четных порядков - положительны.
Теорема 8 (достаточное
условие экстремума функции).
Для того чтобы дважды непрерывно дифференцируемая функция 
имела в
стационарной точке 
локальный
минимум (максимум), необходимо и достаточно, чтобы матрица Гессе в этой точке
была положительно (отрицательно) определена.
Пример 1. Исследовать
на экстремум функцию двух переменных 
.
Решение. Найдем
частные производные функции и приравняем их к нулю:
.
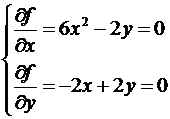Решив систему, получим две стационарные
точки: 
и 
.
Составим матрицу Гессе для первой точки:
,
,
.
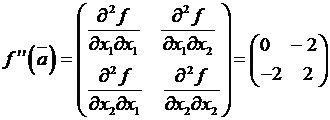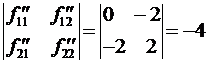Не выполнены условия положительной или отрицательной определенности,
локального экстремума нет.
Составим матрицу Гессе для второй точки:
,
,
.
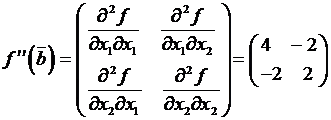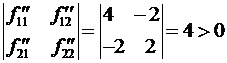Выполнено условие положительной определенности, в точке локальный минимум.
Глобальный максимум
Определение
18.
Точка (x0,
y0) называется точкой абсолютного (глобального) максимума (минимума) на
множестве А Î R2, если значение функции в этой точке больше (меньше) значения
функции в любой точке множества А.
Теорема 9 (теорема Вейерштрасса). Если функция многих переменных непрерывна на
замкнутом ограниченном множестве, то она достигает на нем своего глобального
максимума и глобального минимума.
Если множество ограничено и
замкнуто, то глобальные максимум и минимум непрерывной функции расположены либо
в точках границы множества, либо в стационарных точках функции.
Пример 1.1. Исследовать на наличие экстремумов функцию 
, где 
.
Решение. Находим
стационарную точку:
.
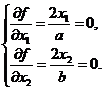
Матрица
Гессе:
.
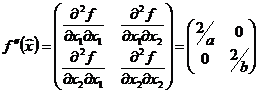Диагональные
миноры:
, 
.
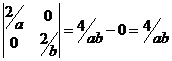Возможны
следующие исходы:
1)
если 
и 
, тогда оба минора положительны, матрица положительно
определена, следовательно, в стационарной точке минимум;
2)
если и 
, тогда второй минор отрицателен, следовательно,
экстремума нет;
3)
если 
и , тогда второй минор отрицателен, следовательно,
экстремума нет;
4)
если 
и , тогда первый минор отрицателен, второй положителен,
матрица отрицательно определена, в стационарной точке максимум.
1. Задачи с
ограничениями-уравнениями.
Функция Лагранжа
Исследуем
на экстремум функцию 
, при условии, что вектор 
удовлетворяет
уравнениям связи 
где 
- непрерывно
дифференцируемые скалярные функции векторного аргумента. Предположим, что 
- решение
задачи
. (1)
В
этом случае говорят, что является точкой
условного максимума функции .
Определение 1. Допустимая точка есть точка
условного максимума функции , если существует такое 
, что для всех 
, удовлетворяющих уравнениям связи и условию 
, выполняется неравенство 
.
Уравнения связи можно было бы использовать для того, чтобы в
некоторой окрестности допустимой точки какие-либо 
переменных
выразить через остальные 
:
. (2)
Это возможно, если в рассматриваемой точке существуют частные
производные и определитель матрицы частных производных (якобиан) не равен нулю,
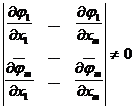. (3)
Тогда
подставляя (2) в целевую
функцию , можно свести исходную задачу к отысканию
безусловного экстремума функции переменных
.
Однако
осуществить такой подход напрямую чаще всего бывает трудно или даже невозможно.
Рассмотрим другой путь, который не предполагает использования явных выражений (2), хотя и опирается на условие (3). Он связан с так называемой функцией Лагранжа
, (4)
где 
- множители
Лагранжа.
Теорема 1. Пусть
точка - решение
задачи (1), и в ее
окрестности выполняется условие (3). Тогда
существует вектор 
такой, что 
представляет
собой стационарную точку функции Лагранжа.
Доказательство. В
стационарной точке полный
дифференциал равен нулю. Запишем это с учетом разделения переменных на
зависимые и независимые:
, (5)
где
- дифференциалы
зависимых переменных, связанные с дифференциалами 
независимых
переменных системой уравнений
, 
. (6)
Исключим
дифференциалы зависимых переменных из уравнений (5), (6). Для
этого умножим каждое из уравнений системы (6) на произвольные множители 
. Результаты сложим с уравнением (5):
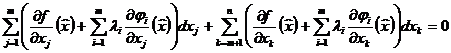. ( 7)
Подберем
множители так, чтобы
коэффициенты при дифференциалах зависимых переменных стали нулевыми:
, 
. (8)
Перепишем
эти условия в виде:
, .
Получили
систему линейных уравнений относительно 
. Эта система имеет единственное решение, поскольку
предполагается, что ее определитель не равен нулю (см. условие (3)).
При
выбранных таким образом множителях в выражении (7) останутся лишь члены, содержащие дифференциалы
независимых переменных.
.
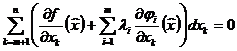Из
чего в силу произвольности 
следует, что
, 
. (9)
Таким
образом, мы получили систему 
уравнений
относительно переменных 
. Это уравнения связи, 
а также
уравнения (8) и (9). Как видим, они совпадают с условиями стационарности
функции Лагранжа:
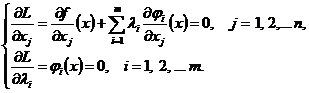
Теорема
доказана.
К
такому же выводу можно прийти, если рассмотреть геометрическую интерпретацию
задачи двух переменных
, 
. (10)
X1
=0
Рис. 1. Графическое представление задачи
Предположим,
что целевая функция представлена совокупностью изоквант (линий постоянного
уровня) 
, где 
(рис. 1.).
Очевидно, найдется изокванта, которая будет иметь с кривой 
точку касания . Эта точка и будет решением задачи, поскольку
смещение из нее по допустимой линии в любом направлении приводит к попаданию на
изокванты более низкого уровня. Заметим, что в этой точке кривые и 
имеют
совпадающие касательные. Следовательно, их градиенты, лежат на одной прямой и
отличаются на постоянный множитель:
. (11)
Таким
образом, в точке выполняются
условия (1) и (11), но это и есть условия стационарности функции
Лагранжа для данной задачи, т.е. функции
.
Метод множителей Лагранжа. Итак,
используя функцию Лагранжа, задачу с ограничениями, заданными с помощью
уравнений, можно свести к безусловной задаче. Метод включает следующие этапы:
1.
Составляем функцию Лагранжа
.
2.
Выписываем необходимые условия:
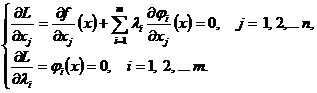
3.
Решаем полученную систему уравнений, находим условно-стационарную точку ,. Заметим, что для решения этой системы, возможно,
потребуется использование численных методов, изложение которых дано ниже.
4. Анализируем выполнение достаточных условий,
проверяем знакоопределенность квадратичной формы функции Лагранжа
.
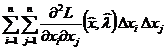Если
получается отрицательный результат, то анализ следует провести для векторов 
, удовлетворяющих системе линейных уравнений
, ,
которые образуются в результате
дифференцирования уравнений связи. Поскольку выполняется условие (1.5), то
можно выразить m переменных через остальные и подставить
полученные выражения в формулу второго полного дифференциала. Затем полученное
выражение, определяемое теперь уже только независимыми приращениями, нужно
вновь исследовать на знакоопределенность.
Пример 1.2. Исследуем
на экстремум функцию 
при
условии 
.
Функция
Лагранжа:
.
Условия
стационарности:
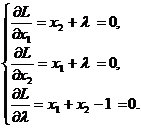
Решение
системы: 
, 
, 
.
Исследуем выполнение условия достаточности, вычислив матрицу
Гессе:
.
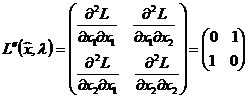Второй
минор отрицателен, следовательно, условие достаточности не выполняется. Но этот
вывод сделан без учета того, что приращения аргументов не независимы, а подчиняются
уравнению связи
.
Вычислим
квадратичную форму с учетом того, что 
:
.
Как видим,
при ненулевых допустимых приращениях квадратичная форма всегда отрицательна.
Значит, исследуемая точка есть точка максимума.
Пример 1.3. Найти
экстремум функции 
при
условии 
.
Действуем
по той же схеме.
.
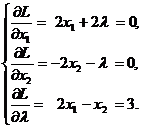
Решение системы:
, 
, 
.
.
, 
.
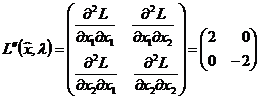Второй
минор отрицателен, следовательно, условие достаточности не выполняется.
Проведем исследование знакоопределенности квадратичной формы с учетом уравнения
связи. Из уравнения связи получаем:
.
Квадратичная
форма:
.
Из
соотношения следует, что 
. Как видим, при ненулевых приращениях,
удовлетворяющих уравнению связи,
квадратичная форма всегда отрицательна. Значит, в стационарной точке
максимум.
Пример 1.4.
(Неоклассическая модель потребления). Потребитель располагает суммой 
, которую тратит на приобретение различных товаров.
Всего имеется 
товаров, цены
которых заданы вектором 
. Если обозначить спрос на товары вектором 
, то задачу потребительского выбора можно
сформулировать так:
,
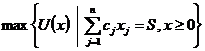где
- функция
полезности, которая представляет собой меру удовлетворенности потребителя
набором 
. Согласно неоклассической теории
,
где
, 
. В этом случае
задача принимает вид
,
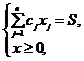
и является в силу свойств
параметров целевой функции выпуклой. Заменим целевую функцию эквивалентной:
.
Приведем
задачу к безусловному виду:
.
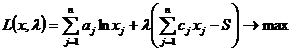Условие
стационарности:
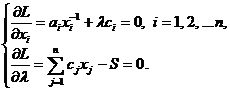
Из первой
группы уравнений следует, что 
. Далее в результате простых выкладок получаем:
, 
.
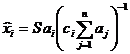Матрица
Гессе:
.
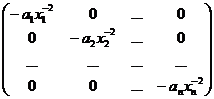Как видим,
все нечетные миноры отрицательны, а четные положительны, следовательно, в стационарной точке находится
максимум.
Метод
множителей Лагранжа не только дает решение задачи, но и позволяет сделать
анализ оптимального состояния. В частности, важную информацию содержат в себе
множители Лагранжа. Они показывают
чувствительность целевой функции к изменению параметров ограничений. В
экономических задачах целевая функция обычно измеряется в единицах стоимости
(выручка, прибыль, издержки), а связи выражают ресурсные ограничения. В таких
задачах можно
интерпретировать как цены ресурсов. Поэтому их еще называют теневыми ценами.