Лекция 3. Функции многих переменных Безусловная оптимизация

1. Понятие функции многих переменных

Пусть даны множества D Rⁿ и I R.

Определение 1. Если каждой точке множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у = f(x₁, …, x_n). Множество D называется областью определения функции D(у) = D, множество I называется множеством значений функции I (у) = I.

Если зафиксировать любые n – 1 переменные, то функция многих переменных превращается в функцию одной переменной. x₂ = с₂, x₃ = с₃, …, х_n = c_n; y = f(x₁, c₂, …, c_n) — функция одной переменной х₁.

Пример 1.

— функция двух переменных,

— функция трех переменных.

Определение 2. Графиком функции двух переменных (рис. 1) z = f(x, y) называется множество точек (х, у, z) 3-мерного пространства, таких, что (х, у) D(z) и z = = f(x, y). Любую точку графика можно записать в виде (х, у, f(x, y)).

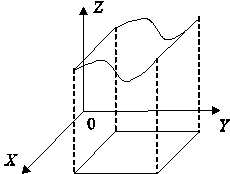
Рис. 1

Определение 3. Графиком функции n переменных называется n-мерная гиперповерхность в пространстве R^{n + 1}, точки которой имеют вид

(х₁, х₂, …, х_n, f(x₁, х₂, …, x_n)).

Определение 4. Линией уровня функции двух переменных называется линия на плоскости XOY, принадлежащая D(z), в каждой точке которой функция принимает одно и то же значение.

Уравнение линии уровня: f(x, y) = c, где с — произвольное число. На данной линии уровня значение функции z = c. Линий уровня бесконечно много, и через каждую точку области определения можно провести линию уровня.

Пример 2. Построить линии уровня функции z(x,y) = ,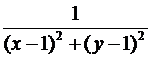

D(z) = R²\{(1,1)}.

c = 1, 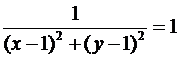, z = 1.

c = 4, 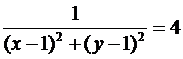, z = 4.

c = 9, 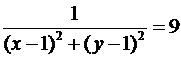, z = 9.

Линиями уровня является семейство концентрических окружностей (рис 2).

Рис. 2

Используя линии уровня, можно построить график функции (рис 3).

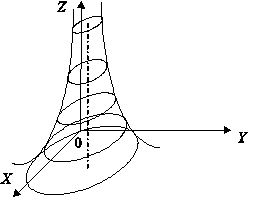
Рис. 3

Определение 5. Поверхностью уровня функции n переменных y = f(х₁, х₂, …, х_n) называется гиперповерхность в пространстве Rⁿ, входящая в D(у), в каждой точке которой значение функции одно и то же. Уравнение поверхности уровня f(х₁, х₂, …, х_n) = с. На поверхности уровня значение функции постоянно: у = с.

2. Непрерывность функции многих переменных

Рассмотрим функцию двух переменных n = 2; z = f(x,y). Возьмем точку (х₀,у₀) D(у) R². Дадим аргументу х в данной точке приращение , зафиксировав у₀. Выражение

называется частным приращением функции по переменной х.

Аналогично, фиксируя х₀ и давая аргументу у приращение , мы получим частное приращение по переменной у.

.

Выражение

называется полным приращением функции.

Определение 6. Функция z = f(x,y) называется непрерывной в точке (x₀,y₀) D(у), если она определена в этой точке и малым приращениям аргументов соответствует малое полное приращение функции.

.

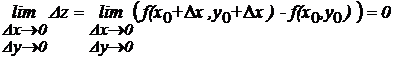Определение 7. Функция z = f(x,y) называется непрерывной на множестве А D(z), если она непрерывна в каждой точке этого множества.

3. Частные производные функции многих переменных

Рассмотрим функцию двух переменных n = 2; z = f(x,y).

Определение 8. Частной производной функции z = f(x,y) в точке (x₀, y₀) D(у) по соответствующей переменной называется предел отношения частного приращения функции по этой переменной к приращению этой переменной, когда приращение переменной стремится к нулю (если этот предел существует и конечен).

,

.

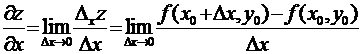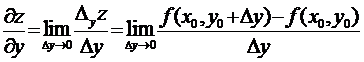При введении частной производной по любой переменной остальные переменные были фиксированы. Данное определение совпадает с определением производной функции одной переменной. Следовательно, частную производную можно найти, зафиксировав все переменные, кроме одной, считая их постоянными. Производная находится как производная функции одной переменной, т.е.

.

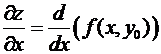Все правила и формулы, справедливые для производной функции одной переменной, остаются справедливыми и для частных производных.

Пример 3.Найдем частные производные функции .

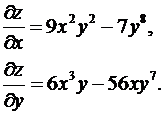
Пример 4. Найдем частные производные функции .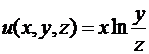

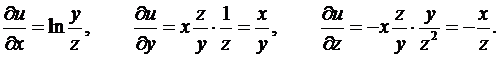
4. Полный дифференциал

Определение 7. Полным дифференциалом функции многих переменных называется главная линейная относительно приращений аргументов часть малого полного приращения функции.

Рассмотрим функцию двух переменных n = 2; z = f(x,y). Если приращение функции

можно представить в виде

, (*)

где — бесконечно малые функции при , соответственно, то выражение называется полным дифференциалом функции двух переменных.

Теорема 1. Полный дифференциал равен сумме произведений частных производных на дифференциалы соответствующих переменных.

.

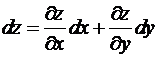Для случая функции n переменных :

.

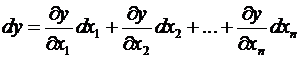Пример 5. Найдем полный дифференциал функции .

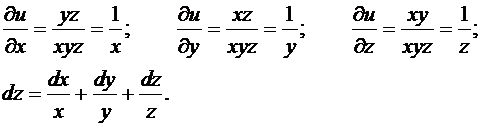
5. Производная по направлению

Рассмотрим функцию двух переменных n = 2; z = f(x, y). Под направлением мы будем понимать любой вектор на плоскости (рис. 4).

Рис. 4

Определение 8. Направляющими косинусами данного направления называются косинусы углов, которые данное направление образует с положительными направлениями осей координат. Направляющие косинусы данного направления — .

Направляющие косинусы любого направления в любом пространстве обладают следующим свойством: сумма квадратов направляющих косинусов равна единице.

.

На плоскости имеем

.

.

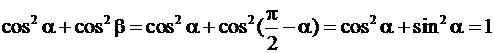Если рассмотреть вектор , координатами которого являются направляющие косинусы данного направления, то этот вектор сонаправлен с вектором и имеет единичную длину.

Пусть даны точка и направление . Переместим точку вдоль направления на величину Dl в точку (рис. 5). Тогда функция и аргумент получат соответствующие приращения.

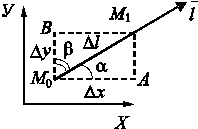
Рис. 5

Функция получит приращение, которое называется приращением функции в данном направлении:

,

Из треугольника : . Из треугольника : .

.

Определение 9. Предел отношения приращения функции в данном направлении к приращению направления, когда приращение направления стремится к нулю, называется производной функции в данном направлении (если этот предел существует и конечен)

.

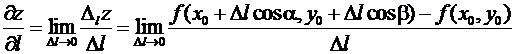Если направление совпадает с направлением оси ОХ, то производная по направлению совпадает с частной производной по переменной х. Аналогично производная по направлению оси ОY совпадает с частной производной по переменной у.

Теорема 2. Производная по направлению равна сумме произведений частных производных в данной точке на направляющие косинусы данного направления.

.

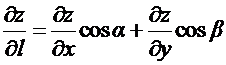Для случая функции n переменных и направления , заданного направляющими косинусами :

.

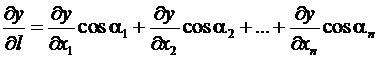Пример 6.

Найдем производную функции в точке М(1, 2) в направлении (4, –3).

.

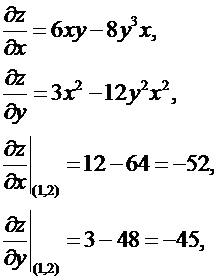
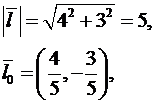
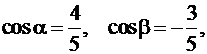
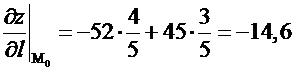6. Градиент функции многих переменных

Рассмотрим функцию трех переменных n = 3, u = f(x, y, z).

Определение 10. Градиентом функции многих переменных в данной точке называется вектор, координаты которого равны частным производным по соответствующим аргументам, вычисленным в данной точке.

.

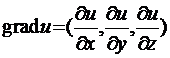Теорема 3. Производная функции в данном направлении равна проекции градиента на данное направление.

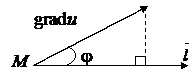
Рис. 6

.

Следствие. Градиент функции в данной точке показывает направление наискорейшего возрастания функции. Модуль градиента совпадает с максимальной скоростью возрастания функции в данной точке.

Теорема 4. Градиент функции в каждой точке области определения направлен по нормали к линии уровня (нормалью к плоской кривой называется перпендикуляр к касательной, проведенной в точку касания) (рис. 7).

Рис. 7

7. Частные производные высших порядков

Рассмотрим функцию двух переменных n = 2, . Предположим, что функция имеет частные производные

, ,

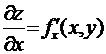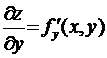которые являются функциями двух переменных. Их называют частными производными первого порядка. Предположим, что они дифференцируемы.

Определение 11. Частные производные от частных производных первого порядка называются частными производными второго порядка.

= , = .

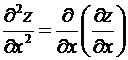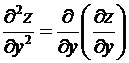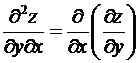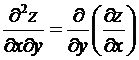= , = — смешанные производные.

Если полученные функции являются дифференцируемыми, то частные производные от них называются частными производными третьего порядка. Например:

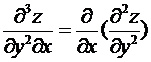и т.д.

Определение 12. Частной производной n-го порядка называется частная производная от частной производной (n – 1)-го порядка. Функция двух переменных имеет 2ⁿ производных n-го порядка.

Частная производная порядка р функции имеет вид

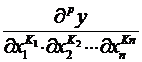, где .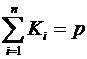

Теорема 5. Если частные производные первого порядка некоторой функции непрерывно дифференцируемы, то результаты смешанного дифференцирования равны.

.

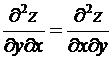Пример 6. Найдем частные производные второго порядка .

, ,

, , ,

,

.
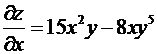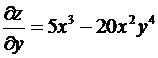
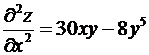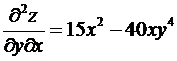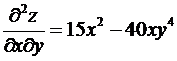
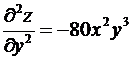
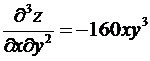