Лекция 2.  Системы линейных уравнений

 

9. Определители

 

Пусть дана квадратная матрица порядка n:

А = .

 

 

 

Определение 26. Определителем n-го порядка матрицы А называется число, равное алгебраической сумме n! слагаемых, каждое из которых равно произведению n элементов матрицы  , взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком «+» или «–».

.

 

 

 

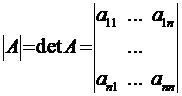Пример . Определитель второго порядка имеет  2! = 1 · 2 = 2 слагаемых.

.

 

 

 

Мнемоническое правило вычисления определителя второго порядка:

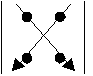
Пример 8

 

 

 

слагаемое со знаком «–»,                         слагаемое со знаком «+»

Пример . Определитель третьего порядка имеет 3! = 1 · 2 · 3 = 6 слагаемых,

 

 

 

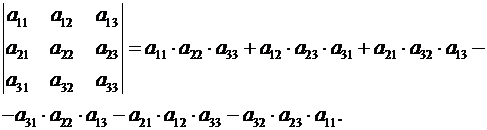
Мнемоническое правило вычисления определителя третьего порядка:

Пример 8

 

 

 

слагаемые со знаком «+»,                    слагаемые со знаком «–»

Можно построить мнемонические правила для вычисления определителей порядка выше, чем три, но они будут слишком громоздкими. Поэтому вычисление таких определителей основано на свойствах определителей.

 

 

10. Свойства определителей

 

Теорема 8. При транспонировании величина определителя не меняется.

Следствие. Строки и столбцы в определителе равноправны, т.е. свойства, справедливые для строк, будут справедливы и для столбцов.

Теорема 9. Если все элементы одной строки определителя умножить на одно и то же число, то и весь определитель умножится на это число.

Следствие. Постоянный множитель строки можно выносить за знак определителя.

Теорема 1.10. Если в определителе поменять местами две строки, то определитель сменит знак на противоположный.

Следствие 1. Определитель, у которого две строки равны, равен нулю.

Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю.

Теорема 11. Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится.

11. Миноры и алгебраические дополнения

 

Пусть дана прямоугольная матрица А размера .

Определение 27. Минором порядка k данной матрицы, где k  min(m;n), называется определитель k-го порядка, полученный из матрицы А вычеркиванием (m – k) строк и (n – k) столбцов.

Определение 28. Дополнительным минором Mij к элементу aij квадратной матрицы  называется определитель (n – 1) порядка, полученный из матрицы А вычеркиванием этого элемента вместе со строкой и столбцом, в которых он расположен.

Определение 29. Алгебраическим дополнением Aij к элементу aij квадратной матрицы  называется число Aij = .

Теорема 12. Определитель равен сумме попарных произведений элементов любой строки (столбца) на их алгебраические дополнения.

 — разложение определителя по i-й строке.

Теорема 13. Сумма попарных произведений элементов любой строки (столбца) определителя на алгебраические дополнения к соответствующим элементам другой строки (столбца) равна нулю.

Вычисление определителей порядка n > 3 сводится к вычислению определителей второго и третьего порядка с помощью теорем 1.12 и 1.13.

 

12. Обратная матрица

 

Определение 30. Квадратная матрица называется вырожденной, если ее определитель равен нулю, и невырожденной — в противном случае.

Определение 31. Матрица А–1 называется обратной к квадратной матрице А n-го порядка, если А·А–1 = А–1·А = Е.

Теорема 14. Для любой невырожденной квадратной матрицы существует единственная обратная матрица.

 

13. Элементарные преобразования над матрицей. Нахождение обратной матрицы

 

Определение 32. Элементарными преобразованиями над матрицей называются:

1)    умножение любой строки на число, отличное от нуля;

2)    прибавление к элементам одной строки соответствующих элементов другой, умноженных на одно и то же число;

3)    перестановка строк;

4)    отбрасывание строки из нулей.

Определение 33. Две матрицы называются эквивалентными (А~В), если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.

Теорема 15. Любую невырожденную квадратную матрицу с помощью элементарных преобразований можно привести к единичной матрице того же порядка. Применяя ту же последовательность элементарных преобразований к единичной матрице, можно получить обратную матрицу к данной.

Обычно элементарные преобразования производят над данной матрицей и единичной одновременно. Для этого составляют расширенную матрицу, в левой части которой стоит исходная матрица, а в правой — единичная матрица того же порядка. С помощью элементарных преобразований в левой части создают единичную матрицу, параллельно в правой части автоматически создается обратная матрица.

.

 

 

14. Ранг матрицы

 

Пусть дана произвольная матрица размером . Возьмем произвольные k строк и k столбцов, . Минором порядка k называют определитель порядка k, составленный из элементов, расположенных на пересечении выбранных k строк и k столбцов, и обозначают Mk.

Для данной матрицы можно составить m · n миноров первого порядка,  миноров второго порядка и т.д.,  миноров k-го порядка.

Определение 34. Рангом матрицы называется максимальный порядок минора, отличного от нуля, и обозначается r(A).

Очевидно, что .

15. Системы линейных уравнений

Определение 35. Система вида

 

 

 

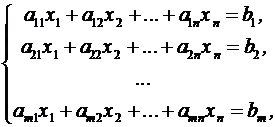
называется системой m линейных уравнений с n неизвестными, где x1, x2, …, xn — неизвестные, aij, i = , j =  — коэффициенты при неизвестных, b1, b2, …, bm — свободные члены.

Определение 36. Если все свободные члены равны нулю, то система называется однородной, и неоднородной — в противном случае.

Определение 37. Решением системы называется совокупность из n чисел с1, с2, …, сn, при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств.

Определение 38. Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.

Определение 39. Совместная система называется определенной, если она имеет единственное решение, и неопределенной — в противном случае.

При изучении систем исследуют три вопроса:

1)    совместна система или нет;

2)    если система совместна, то является ли она определенной или неопределенной;

3)    нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной.

 Матричная форма записи системы

Пусть дана система

 

 

 

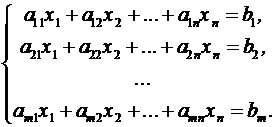
Рассмотрим матрицы

, , .

 

 

 

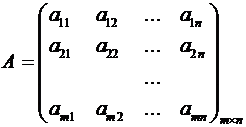С помощью этих матриц систему можно записать в виде .

,

 

 

 

.

 

 

 

 

 

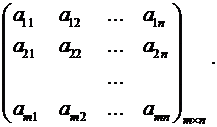
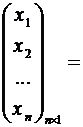
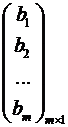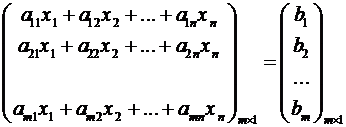Условие совместности

Рассмотрим неоднородную систему:

 

 

 

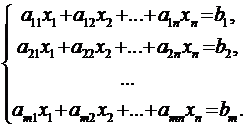
Рассмотрим матрицы:

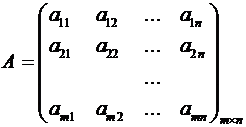 и .

 

 

 

Матрица  называется расширенной матрицей системы.

Теорема 16. (теорема Кронекера-Капелли). Неоднородная система линейных уравнений совместна тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы.

16. Решение произвольных систем линейных неоднородных уравнений

Пусть дана неоднородная система m линейных уравнений с n неизвестными

 

 

 

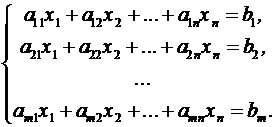
Предположим, что система совместна, т.е. r(A) =  = r. Следовательно, существует минор порядка r матрицы А, отличный от нуля. Предположим, что он расположен в левом верхнем углу матрицы. Если это не так, то можно переставить уравнения и перенумеровать неизвестные.

.

 

 

 

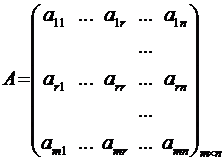Первые r уравнений системы линейно независимы. Остальные выражаются через них. Следовательно, их можно отбросить.

 

 

 

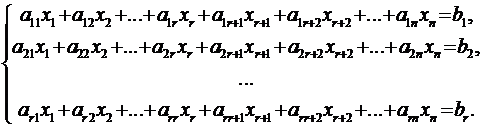
Определение 40. Переменные, коэффициенты при которых образуют минор, отличный от нуля (базисный минор), называются базисными переменными (x1, x2, …, xr). Остальные переменные xr + 1, …, xn называются свободными.

Дадим свободным переменным произвольные числовые значения xr + 1 = сr + 1, xr + 2 = сr + 2, …, xn = cn.

Запишем систему в виде

 

 

 

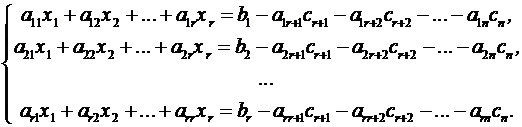
Мы получили систему из r линейных уравнений с r неизвестными, определитель которой отличен от нуля. Она имеет единственное решение.

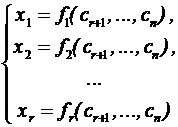 — общее решение.

 

 

 

Определение 41. Выражение базисных переменных через свободные называется общим решением системы.

Определение 42. Решение системы, полученное из общего при конкретных значениях свободных переменных, называется частным решением. Частных решений у системы бесконечно много, все они содержатся в общем решении.

Определение 43. Частное решение, полученное из общего, когда свободные переменные равны нулю, называется базисным решением системы.

Определение 44. Базисное решение, координаты которого неотрицательны, называется опорным решением системы.

 

17. Метод Гаусса

 

Определение 45. Элементарными преобразованиями системы называются:

1)    умножение уравнения на число, отличное от нуля;

2)    прибавление к одному уравнению другого уравнения, умноженного на некоторое число, отличное от нуля.

3)    перестановка двух уравнений;

4)    отбрасывание уравнения 0 = 0.

Если получено уравнение 0 = k, то система несовместна.

Метод Гаусса состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных. Количество исключенных неизвестных равно числу линейно независимых уравнений. Переменная считается исключенной, если она содержится только в одном уравнении с коэффициентом 1.

Таблицы Гаусса

Расширенную матрицу системы записывают в таблицу Гаусса, которая имеет на два столбца больше, чем число неизвестных. Расширенные матрицы располагаются в таблице одна под другой. От одной матрицы к другой переходят с помощью преобразований Жордана:

1)       выбирается ключевой элемент преобразования. В качестве ключевого элемента может быть взят любой коэффициент при любой переменной, не равный нулю. Строка и столбец, в которых он располагается, называются ключевыми;

2)       элементы ключевой строки делятся на ключевой элемент;

3)       ключевой столбец заполняется нулями;

4)       остальные элементы пересчитываются по правилу прямоугольника: составляется прямоугольник, в двух вершинах которого находится ключевой элемент (к.э.) и пересчитываемый элемент (п.э.); из произведения элементов, стоящих на диагонали прямоугольника с ключевым элементом, вычитается произведение элементов второй диагонали и полученная разность делится на ключевой элемент.

.

 

 

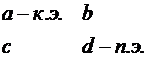
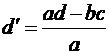Если в ключевой строке (столбце) есть ноль, то соответствующий столбец (строка) при преобразовании Жордана сохраняются.

 

Нахождение неотрицательных базисных решений системы

 

Так как не всякое базисное решение является опорным, то возникают вычислительные затруднения при нахождении опорных решений системы обычным методом Гаусса. Приходится находить все базисные решения и из них выбирать опорные. Существует алгоритм, позволяющий сразу находить опорные решения.

1.    При заполнении исходной таблицы Гаусса все свободные члены делают неотрицательными.

2.    Ключевой элемент выбирается специальным образом:

а) в качестве ключевого столбца выбирают любой столбец коэффициентов при неизвестных, если в нем есть хотя бы один положительный элемент;

б) в качестве ключевой строки берется та, у которой отношение свободного члена к положительному элементу ключевого столбца минимально.

На пересечении ключевой строки и ключевого столбца находится ключевой элемент. Далее проводят обычное преобразование Жордана.