Лекция 1. Элементы линейной алгебры.

1. Линейное векторное пространство

Определение 1. Упорядоченная совокупность из n действительных чисел а₁, а₂, …, а_n называется n-мерным вектором ā(а₁, а₂, …, а_n). Числа а₁, а₂, ..., а_n называются координатами вектора.

Два n-мерных вектора (а₁, а₂, …, а_n) и (b₁, b₂, …, b_n) считаются равными, если равны их соответствующие координаты:

, ().

Вектор, все координаты которого равны нулю, называется ноль-вектором и обозначается .

Определение 2. Суммой (разностью) двух n-мерных векторов (а₁, а₂, …, а_n) и (b₁, b₂, …, b_n) называется n-мерный вектор, координаты которого равны суммам (разностям) соответствующих координат исходных векторов:

= (a₁ b₁; a₂ b₂; …; a_n b_n).

Определение3. Произведением n-мерного вектора (а₁, а₂, …, а_n) на число k называется n‑мерный вектор, координаты которого равны произведениям координат вектора на число k:

k· = (ka₁; ka₂; …; ka_n).

Свойства операций над векторами:

1) + = + — коммутативность,

2) + ( + ) = ( + ) + — ассоциативность,

3) k·() = k· k· — дистрибутивность,

4) (k₁ k₂)· = k_{1 ·} k₂·,

5) (k₁·k₂)· = k₁·(k₂·),

6) 1· = ,

7) 0· = ,

8) k· = ,

9) .

Определение 1.4. Совокупность всех n-мерных векторов с введенными на ней операциями сложения и умножения на число называется n-мерным линейным векторным пространством и обозначается Eⁿ.

2. Скалярное произведение. Длина вектора. Угол между векторами

Определение 5. Скалярным произведением двух n-мерных векторов (а₁, а₂, ..., а_n) и (b₁, b₂, ..., b_n) называется число, равное сумме попарных произведений соответствующих координат.

· = а₁·b₁ + a₂·b₂ + … + a_n·b_n.

Свойства скалярного произведения:

1. · = · — коммутативность;

2. ·( + ) = · + · — дистрибутивность;

3. k·(·) = (k·)·,

4. · = ², ² = 0.

Определение 6. Длиной n-мерного вектора называется величина:

.

Определение 7. Углом между двумя ненулевыми n-мерными векторами называется угол, косинус которого вычисляется по формуле

.

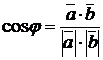3. Системы векторов

Пусть дана система n-мерных векторов .

Определение 8. Линейной комбинацией системы векторов называется выражение вида

,

где с₁, с₂, …, с_k — некоторые числа.

Определение 9. Вектор разлагается по системе векторов , если его можно представить в виде линейной комбинации векторов этой системы.

.

4. Линейная зависимость векторов

Определение 10. Система векторов называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой — в противном случае.

Определение 11´. Система векторов называется линейно зависимой, если найдутся числа с₁, с₂, …, с_k, не все равные нулю, такие, что линейная комбинация векторов с данными коэффициентами равна нулевому вектору: = , в противном случае система называется линейно независимой.

Определение 12. Единичным вектором, или ортом, называется n-мерный вектор, у которого i-я координата равна единице, а остальные — нулевые.

(1, 0, 0, …, 0),

(0, 1, 0, …, 0),

…

(0, 0, 0, …, 1).

Теорема 1. Различные единичные векторы n-мерного пространства линейно независимы.

Каждый вектор n-мерного пространства (а₁, а₂ , ..., а_n) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора

.

Теорема 2. Если система векторов содержит нулевой вектор, то она линейно зависима.

Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.

Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Доказательство. Каждый n-мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m > n, то, по теореме, данная система линейно зависима.

5. Ранг и базис системы векторов

Определение 13. Рангом системы векторов называется максимальное число линейно независимых векторов системы.

.

Определение 14. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.

Теорема 5. Любой вектор системы можно представить в виде линейной комбинации векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.

6. Ранг и базис n‑мерного линейного векторного пространства

Теорема 6. Ранг n-мерного пространства равен его размерности: r = n.

Следствие 1. Любой базис n-мерного пространства состоит из n линейно независимых n-мерных векторов.

Следствие 2. Любая система в n-мерном пространстве, содержащая больше чем n векторов, линейно зависима.

Следствие 3. Любой вектор пространства можно однозначно разложить по векторам любого базиса. Коэффициенты разложения для данного вектора и данного базиса определяются единственным образом. Коэффициенты разложения называются координатами данного вектора в этом базисе.

7. Матрицы

Определение 15. Прямоугольная таблица чисел вида

называется прямоугольной матрицей размера , где m — количество строк, а n — количество столбцов.

Определение 16. Числа, которые образуют матрицу, — a_ij, где , , называются элементами матрицы.

Определение 17. Числа i и j называются индексами элемента a_ij, i показывает, в какой строке расположен данный элемент, а j — в каком столбце находится этот элемент.

Две матрицы считаются равными, если равны их соответствующие элементы.

Виды матриц

Если m = n, то матрица называется квадратной матрицей порядка n.

Матрица размера называется матрицей-столбцом.

.

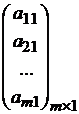Матрица размера называется матрицей-строкой.

.

Определение 18. Элементы матрицы, имеющие равные индексы, образуют главную диагональ матрицы.

Определение 19. Квадратная матрица называется диагональной, если все элементы вне ее главной диагонали равны нулю.

Определение 20. Диагональная матрица n-го порядка, у которой диагональные элементы равны единице, называется единичной матрицей n-го порядка и обозначается Е.

Определение 21. Матрица называется матрицей треугольного вида, если все элементы над (под) главной диагональю равны нулю

8. Операции над матрицами

Определение 22. Транспонированием матрицы называется такое преобразование матрицы, при котором строки и столбцы меняются ролями при сохранении номеров. Транспонированная матрица обозначается А^Т.

, , .

Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали.

Определение 23. Суммой (разностью) двух матриц одинакового порядка называется матрица того же порядка, каждый элемент которой равен сумме (разности) соответствующих элементов исходных матриц.

, , .

Определение 24. Произведением матрицы на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента исходной матрицы на это число.

, , .

Определение 25. Произведением двух матриц А и В, размеры которых заданы соотношением: количество столбцов первой матрицы равно количеству строк второй, называется матрица С, у которой количество строк равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй. Каждый элемент данной матрицы равен сумме попарных произведений элементов соответствующей строки первой матрицы и элементов соответствующего столбца второй.

, , , .

Приведем основные свойства операций над матрицами.

1.	А · В В · А	— произведение матриц не коммутативно.
2.	А + В = В + А	— сложение матриц коммутативно.
3.	(А + В) + С = А + (В + С)	— ассоциативность сложения.
4.	(А В) С = А (В С)	— ассоциативность умножения.
5.	,
6.	,
7.	,
8.		— правая дистрибутивность.
9.		— левая дистрибутивность.
10.	А · Е = Е · А = А.
11.	.
12.	.
13.	.