Миноры и алгебраические дополнения
Пусть дана прямоугольная матрица А размера 
.
Определение 1. Минором порядка k данной матрицы, где k
min(m;n), называется определитель k-го порядка, полученный из матрицы А
вычеркиванием (m-k) строк и (n-k) столбцов.
Пример. А=
, 
,
.
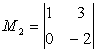Определение
2. Дополнительным минором Mij к элементу aij квадратной матрицы 
называется
определитель (n-1)
порядка, полученный из матрицы А
вычеркиванием этого элемента вместе со строкой и столбцом, в которых он
расположен.
Пример.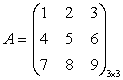 
.
Найдем
дополнительный минор к элементу a31. 
.
Определение
3. Алгебраическим дополнением Aij к элементу aij квадратной матрицы 
называется число Aij=
.
Пример. Найдем алгебраическое дополнение к элементу a33.
.
Теорема 1. Определитель равен сумме попарных произведений элементов любой строки на их алгебраические дополнения.
- разложение
определителя по i-й
строке.
Теорема 2. Сумма попарных произведений элементов любой строки определителя на алгебраические дополнения к соответствующим элементам другой строки равна нулю.
Вычисление определителей порядка n>3 сводится к вычислению определителей второго и третьего порядка с помощью теоремы 1 и свойства 5 определителя.
разложение
определителя по первому столбцу
Пример.
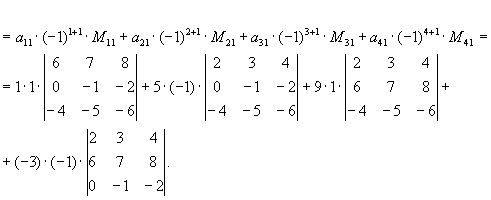
Перед разложением определителя для удобства получают в одном из столбцов нули. Это сокращает объемы вычислений. Для этого используют пятое свойство определителя. Одну из строк умножают на некоторые числа и складывают с другими строками.
